Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 12

Sabendo que A 1 , - 1 , B 5,1 e C 6,4 são vértices de um paralelogramo, determinar o quarto vértice de cada um dos três paralelogramos possíveis de serem formados.

Passo 1

Primeiro vamos ver graficamente esses pontos para analisar melhor:

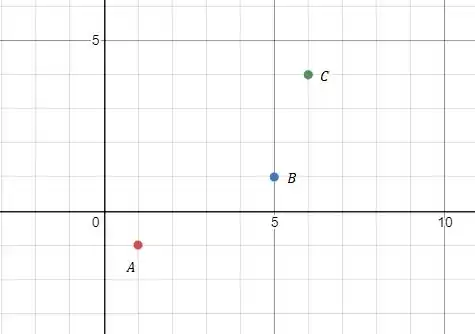
Podemos ver que para ter o paralelogramo A B C D vamos poder ter o vértice D no primeiro quadrante, próximo do eixo y , tendo os seguimentos:

A B - = D C -

A segunda maneira para ter o paralelogramo A B C D é ter o vértice D no quarto quadrante, tendo os seguimentos:

A C - = D B -

E a terceira maneira é ter o vértice D novamente no primeiro quadrante, mas aqui longe do eixo y , distante do ponto C , temos assim os seguimentos:

A C - = B D -

Assim podemos fazer a comparação dos segmentos do paralelogramo, igualando os dois lados, vamos então achar o vértice D para cada um dos três paralelogramos possíveis de serem formados.

Passo 2

Na primeira maneira, para achar D temos que os segmentos A B - deve ser igual a C D - , vamos então achar o vértice D :

A B - = D C - → B - A = C - D → D = C - B + A →

→ D = 6,4 - 5,1 + 1 , - 1 →

→ D = 6 - 5 + 1 , 4 - 1 + - 1 = 2 , 3 - 1 = 2 , 2

Pronto, temos que o vértice oposto a B é D = 2 , 2 .

Vamos ver o paralelogramo A B C D :

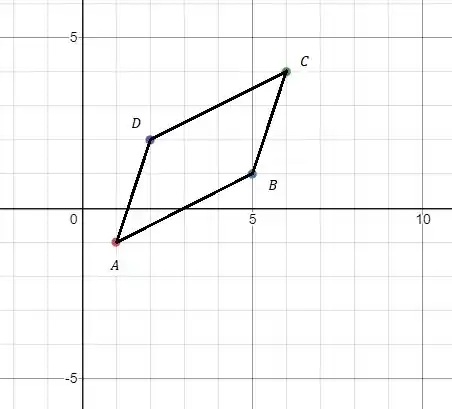
Passo 3

Na segunda maneira, para achar D temos que os segmentos A C - deve ser igual a D B - , vamos então achar o vértice D :

A C - = D B - → C - A = B - D → D = B - C + A →

→ D = 5,1 - 6,4 + 1 , - 1 →

→ D = 5 - 6 + 1 , 1 - 4 + - 1 = 0 , - 3 - 1 = 0 , - 4

Pronto, temos que o vértice oposto a B é D = 0 , - 4 .

Vamos ver o paralelogramo A B C D :

Passo 4

E a terceira maneira, para achar D temos que os segmentos A C - deve ser igual a B D - , vamos então achar o vértice D :

A C - = B D - → C - A = D - B → D = C - A + B →

→ D = 6,4 - 1 , - 1 + 5,1 →

→ D = 6 - 1 + 5 , 4 - - 1 + 1 = 1 0 , 5 + 1 = 1 0 , 6

Pronto, temos que o vértice oposto a B é D = 10,6 .

Vamos ver o paralelogramo A B C D :

Resposta

D = 2,2 , D = 0 , - 4 e D = 10,6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:a) x → = B A → + 2 B C →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:b) x → = 2 C A → + 2 B A →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:c) x → = 3 A B → - 2 B C →
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor x → nos casos:d) x → = 1 2 A B → - 2 C B →
8) Dados os veotres u → e v → da figura 1.32, mostrar, em um gráfico, um representante do vetorb) v → - u →