Calule a razão de amplitude e o ângulo de fase para a resposta considerando a função de transferência abaixo:
A entrada é senoidal e tem a seguinte forma:
Dê a expressão da resposta .
Passo 1
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
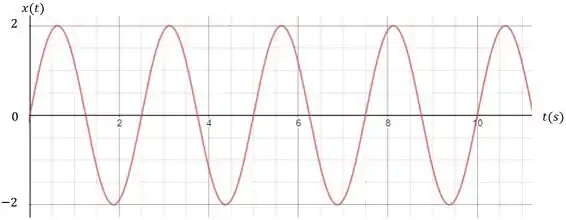
Pelo gráfico podemos ver que a entrada efetua um ciclo a cada , sendo assim, a frequência em hertz será:
Para passar para :
Substituindo na função de transferência:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser reescrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser reescrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Passo 4
A resposta terá a seguinte forma:
A frequência, , será a mesma da frequência da entrada, então:
O ângulo de fase já foi calculado:
Já para calcular a amplitude, devemos usar a definição de razão de amplitude, que é a razão entra a amplitude da saída pela amplitude de entrada
A razão de amplitude já foi calculada e a amplitude da entrada pode ser obtida pelo gráfico, sendo assim:
A expressão da resposta será, então: