Determine a rotação das seguintes molas da seguinte viga. .
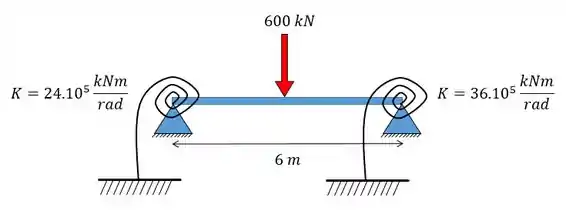
Passo 1
A primeira coisa que devemos fazer é determinar as deslocabilidades internas, que no nosso caso podemos ver que se tratam de apoios extremos de uma viga e que em teoria não teria deslocabilidades internas, certo? Porém lembre-se da nossa nova regrinha que no lugar das molas do tipo engaste elástico devemos colocar chapas, sendo assim a nossa estrutura será:
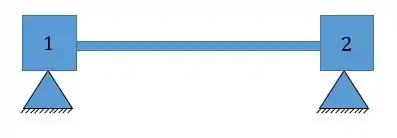
Passo 2
Vimos também no início dessa aula que para o sistema zero solucionamos o nosso problema como se não existisse a mola, ou seja, basta determinarmos os valores de e . Para isso temos:
- Perceba que a barra possui chapa de ambos os lados, e ela possui apenas uma carga concentrada, sendo assim nossa tabela será:
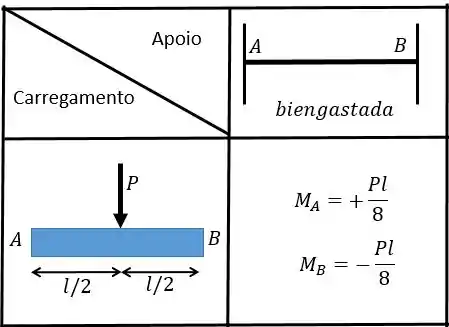
Portanto, utilizando a tabela nós vamos ter:
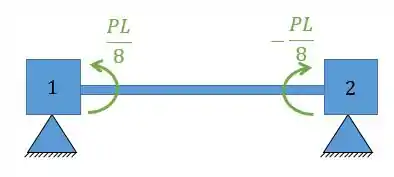
Onde:
Com isso teremos que:
Passo 3
Sabemos que para solucionarmos o sistema 1, basta que rotacionemos a chapa 1, e com isso teremos como determinar o . Lembrando que sempre rotacionamos a nossa chapa no sentido anti-horário para mantermos o sinal positivo e sendo assim teremos a seguinte tabela a ser usada para a barra respeitando o caso Bi-engastado:
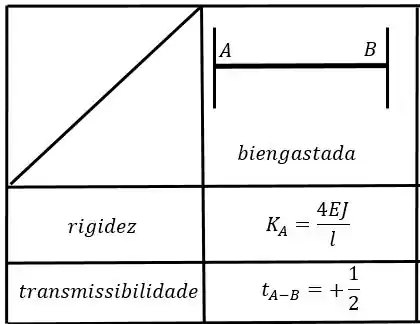
E rotacionando a chapa 1 e aplicando as equações teremos:

Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Maaaaaaaaaaaaaas é aqui que devemos tomar o nosso cuidado. Lembra que tanto a chapa 1 quanto 2 são uma mola? E que rotacionamos, nesse caso a chapa 1, que é essa mola em 1 radiano? Ou seja, temos que somar esse momento gerado ao fator mas não ao fator . Porque não somamos ao se ele é uma mola? Porque só temos certeza da rotação que aconteceu na chapa 1, que foi uma rotação de 1 radiano que nós mesmos colocamos. A rotação da segunda mola vai ser contabilizada, quando rotacionarmos a segunda mola.
Como sabemos, a fórmula a ser usada é:
Temos que tomar cuidado de usar nesse caso o K da mola que rotacionamos, nesse caso, a mola representada pela chapa 1.
Somando teremos que:
Usando o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 4
Sabemos que para solucionarmos o sistema 2, basta que rotacionemos a chapa 2, e com isso teremos como determinar o . Lembrando que sempre rotacionamos a nossa chapa no sentido anti-horário para mantermos o sinal positivo e sendo assim teremos a seguinte tabela a ser usada para a barra respeitando o caso Bi-engastado:
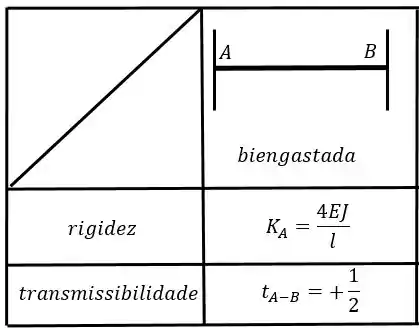
E rotacionando a chapa 2 e aplicando as equações teremos:
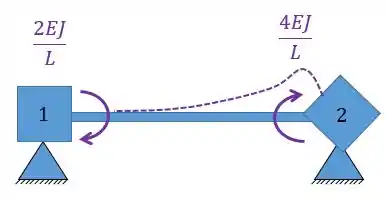
Veja que temos:
Usando o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Maaaaaaaaaaaaaas é aqui que devemos tomar o nosso cuidado. Lembra que tanto a chapa 1 quanto 2 são uma mola? E que rotacionamos, nesse caso a chapa 2, que é essa mola, em 1 radiano? Ou seja, temos que somar esse momento gerado ao fator mas não ao fator . Porque não somamos ao se ele é uma mola? Porque só temos certeza da rotação que aconteceu na chapa 2, que foi uma rotação de 1 radiano que nós mesmos colocamos. A rotação da primeira mola foi contabilizada, quando rotacionarmos a primeira mola.
Como sabemos, a fórmula a ser usada é:
E tome cuidado de usar o k da mola que foi girada, que nesse caso é a mola representada pela chapa 2.
Somando teremos que:
Usando o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 5
Resolvendo o nosso sistema principal teremos que:
Substituindo:
Assim teremos que:
Lembre-se que o objetivo era a deformação na mola, certo? Ou seja, precisamos de , mas precisamos multiplicar ele pelo nosso fator de rigidez (porque utilizamos a rigidez relativa):