Exercícios Resolvidos de Apoios Elásticos em estruturas com deslocabilidade externa
Ver TeoriaEnunciado
Para a viga abaixo com uma mola vertical em B, determine a deformação vertical na mola.
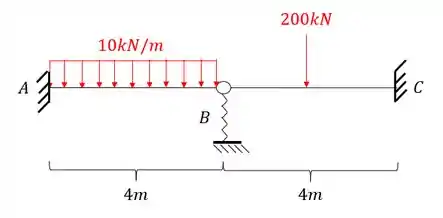
Passo 1
Pela nossa teoria temos que lembrar que o travamento da estrutura é feito levando em conta as deslocabilidades.
- Deslocabilidade Interna
- Temos um engaste em A e C logo nesses pontos não precisamos por chapas de travamento da nossa estrutura.
- No ponto B temos uma rótula, e sabemos que todo nó com rótula não precisa de chapa também.
- Com isso não temos deslocabilidades internas
- Deslocabilidade Externa
- Os pontos A e C são engastes, logo, também não tem deslocabilidade externa
- O ponto B é uma mola, logo, consideramos ela como um ponto propício a se deslocar, e com isso precisamos travar ele.
- E pra fazermos isso precisamos trocar a nossa mola por um apoio do primeiro gênero (lembrando ainda que se trata de uma mola e por isso teremos que fazer um acréscimo em algum momento)
Com isso teremos que:
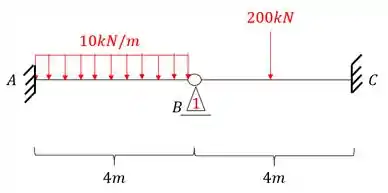
Passo 2
Determinando a deslocabilidade e o que ela é precisamos determinar o que é , e sabemos que como se trata de um apoio do primeiro gênero, iremos precisar da reação de apoio.
Para definirmos a reação de apoio precisamos do passo a passo completo.
- Primeiro determinamos a fórmula
- Segundo definimos os momentos na nossa estrutura
- Determinando as reações de apoio
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E isso é bem simples, a barra AB possui um engaste em A e um apoio em B, logo, engaste e apoio. E para a barra BC acontece a mesma coisa. E como em ambas temos uma carga distribuída por toda viga, a nossa fórmula será.
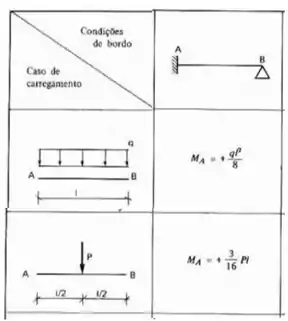
Aplicando na nossa estrutura teremos que:
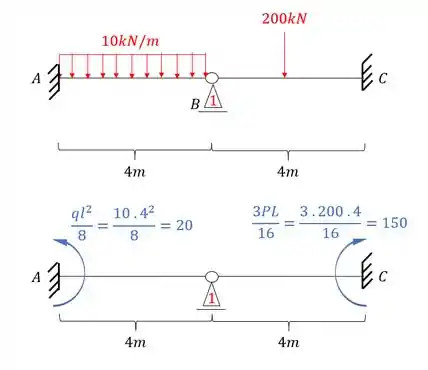
Lembre-se que como temos um apoio do primeiro gênero, precisamos determinar a reação de apoio, dessa maneira teremos que:
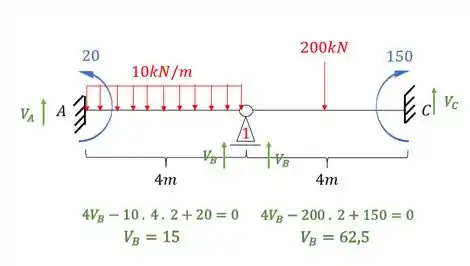
Perceba que a reação deu de baixo pra cima, que é o nosso sentido positivo. E também podemos ver que temos 2 reações de apoio na mesma direção, sendo assim teremos que:
Passo 3
Agora só precisamos do valor de . Como se trata de um apoio do primeiro gênero só precisamos deslocar ele de uma unidade no sentido que definimos como positivo.
Lembre-se que quando usamos deslocamentos impostos usamos a seguinte fórmula:
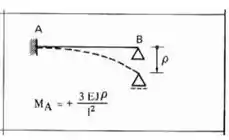
Deslocando a nossa viga teremos que:
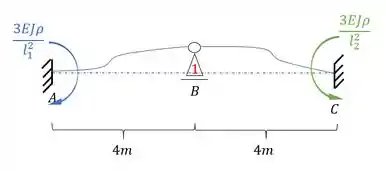
Podemos também dividir tudo por EJ, e lembrar que estamos usando , assim a nossa estrutura passa a ser:
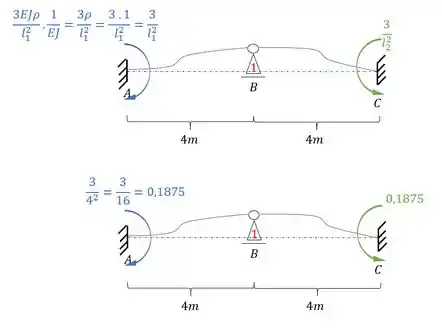
Como o nosso objetivo são as reações de apoio, vamos determinar elas:
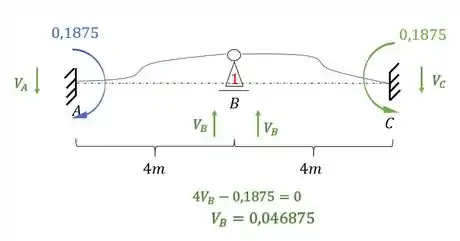
Como temos duas reações de apoio, pra cima, que é o sentido positivo, podemos determinar muito facilmente o valor de , sendo assim teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 3
Resolvendo o nosso sisteminha, teremos que:
Mas lembre-se que a gente dividiu todos os termos por EJ, ou seja, se quisermos definir a deformação final na mola, precisamos dividir o nosso por EJ