Placas de orifício com bordas em canto (ou faca) são muito utilizadas na medição da vazão de fluidos através de tubulações. A figura a seguir mostra uma placa de orifício, que tem os seguintes parâmetros geométricos representativos:
O coeficiente é função da razão , e valores experimentais desse coeficiente estão listados na tabela a seguir:
![]()
a) Fazendo , ajuste a função pela função: aos pontos da tabela, usando o método dos mínimos quadrado.
b) Faça um gráfico dos valores fornecidos pelo polinômio. Acrescente a esse gráfico os valores dos pontos da tabela. Comparando visualmente a curva dos valores fornecidos pelo polinômio, e os valores da tabela, você pode concluir que a aproximação obtida é boa?
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide dadas as placas de orifício com bordas em canto (ou faca) são muito utilizadas na medição da vazão de fluidos através de tubulações. A figura a seguir mostra uma placa de orifício, que tem os seguintes parâmetros geométricos representativos:
O coeficiente é função da razão , e valores experimentais desse coeficiente estão listados na tabela a seguir:
![]()
a) Fazendo , ajuste a função pela função: aos pontos da tabela, usando o método dos mínimos quadrado.
b) Faça um gráfico dos valores fornecidos pelo polinômio. Acrescente a esse gráfico os valores dos pontos da tabela. Comparando visualmente a curva dos valores fornecidos pelo polinômio, e os valores da tabela, você pode concluir que a aproximação obtida é boa?

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha com base nos dados colocados na tabela no passo anterior temos que na letra (a) para,
Com,
Ficando para,
Chegando em,
Ficando,
Já na letra (b) com base dos valores fornecidos temos sua definição gráfica composta por,
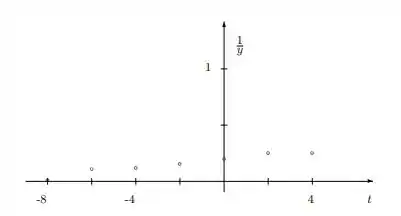

Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b) gráfico demonstrado no passo anterior.