Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 7.Exercícios - Ex. 8
8. A regra dos Retângulos repetida é obtida quando aproximamos , em cada subintervalo, por um polinômio de interpolação de grau zero. Encontre a regra dos Retângulos bem como a expressão do erro, fazendo:
a)
b)
Esta é a regra do ponto médio e é uma fórmula de Newton-Cotes
Passo 1
E aí meu bom! Se liga só! Vamos tentar aí desvendar a regra dos retângulos!
Seja o intervalo finito no eixo x que é particionado em n subintervalos igualmente espaçados , com e e .
Seja uma função contínua ou simplesmente Riemann integrável, cuja integral não é conhecida
Nosso objetivo é calcular pelo método da área dos retângulos.
Passo 2
Tem três modos da gente fazer isso...
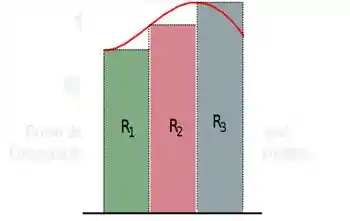
Nesse primeiro caso, a área de cada retângulo é . Outra hipótese seria que...
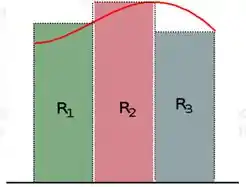
Aí em cima, a área de cada retângulo é ! E há também o caso onde a área do é dada por...
Passo 3
Em todo caso, a soma das áreas dos retângulos será uma aproximação para:
Subdividindo o intervalo em subintervalos, pela regra dos retângulos, que será indicado por , é dada pelas fórmulas:
Como é constante, então...
E obtemos que...
Mas em geral, se usa a seguinte fórmula...