Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 7

7. O número de bactérias por unidade de volume, existente em uma cultura após x horas é apresentado na tabela:

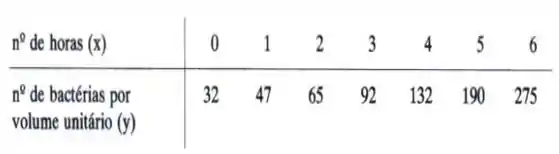
a) Verifique que uma curva para se ajustar ao diagrama é do tipo exponencial

b) ajuste aos dados as curvas y = a b x e y = a x b ; compare os valores obtidos por meio destas equações aos dados experimentais;

c) avalie da melhor forma o valor de y ( x ) para x = 7 .

Passo 1

a) E ai meu bom! Bora pra sexta questão desse capítulo 6!

Se liga só! A função de aproximação, que o exercício pede é a exponencial!

Pois muito bem! Ela é dada por...

ϕ x = c 1 e c 2 x

Com base em uma variável auxiliar z , linearizando, ficamos com...

z = l n ⁡ ( y )

Sendo assim, podemos montar a seguinte com base na que nos foi fornecida pelo enunciado...

Passo 2

E então, plotando os pontos num gráfico, temos que...

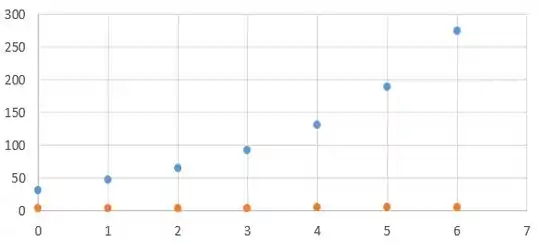
Onde os pontos em azul e laranja, representam respectivamente o antes e depois da linearização.

E como podemos ver, os pontos ficaram bem linearizado e próximos de formar uma reta! Então, o ajuste exponencial acaba sendo bem eficiente!

Passo 3

b) Bora lá pra essa segunda letra! A primeira curva, nós sabemos que é dada por...

y = a b x

Linearizando, temos que...

z 1 = ln ⁡ y = ln ⁡ ( a b x ) = ln ⁡ a + ln ⁡ b x = ln ⁡ a ⏟ c 1 + x ln ⁡ b ⏟ c 2 = c 1 + x c 2

E chegamos até a tabela abaixo...

Onde temos os vetores...

h - 1 = ( 1,1 , 1,1 , 1,1 , 1 )

h - 2 = ( 0,1 , 2,3 , 4,5 , 6 )

f - = ( 3.466,3.85,4.1743,4.522,4.883,5.247,5.617 )

Montando a matriz A ...

A = < h - 1 , h - 1 > < h - 1 , h - 2 > < h - 2 , h - 1 > < h - 2 , h - 2 > = 7 26 26 91

E o vetor b :

b = < f - , h - 1 > < f - , h - 2 > = 31.759 105.231

Obtemos que...

a = 32.147

b = 1.427

Logo...

y = 32.147 ⋅ 1.427 x

Passo 4

Em relação, à segunda curva, temos que...

y = a x b

Linearizando...

z 2 = ln ⁡ y = ln ⁡ ( a x b ) = ln ⁡ a + ln ⁡ x b = ln ⁡ a + b ln ⁡ x

Aqui, é preciso fazer um pequeno ajuste! Tá vendo aquele ln ⁡ x ali!

Pois bem! Vamos chama-lo de x 2 ! A nossa função linearizado então vai ficar assim...

z 2 = ln ⁡ a ⏟ c 3 + b ⏟ c 4 ln ⁡ x ⏟ x 2 = c 3 + c 4 x 2

De modo que a nossa tabela vai ter a seguinte cara...

E temos então, os vetores...

temos os vetores...

h - 3 = ( 1,1 , 1,1 , 1,1 , 1 )

h - 4 = ( I n d e t e r m i n a ç ã o , 0,0.6931 , 1.0986,1.3862,1.6094,1.7917 )

f - = ( 3.466,3.85,4.1743,4.522,4.883,5.247,5.617 )

Obtemos assim, que...

a = 38.83871

b = 0.9630

Logo...

y = 38.83871 ⋅ x 0.963

Passo 5

c) Pela primeira função, temos que y ( 7 ) é...

y = 32.147 ⋅ 1.427 x

y = 32.147 ⋅ 1.427 7

y ≅ 387.35

Pela segunda função, por sua vez, obtemos que...

y = 38.83871 ⋅ x 0.963

y = 252.98

Ou seja, a linearização por a b x acaba se demonstrando muito mais eficiente do que a x b . Convenhamos que 252.98   foi um valor bem fora da casinha, né?

Resposta

a)

y = 32.147 ⋅ 1.427 x

b)

y = 38.83871 ⋅ x 0.963

c)

y ≅ 387.35

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando método dos mínimos quadrados aproxime a função f x =3x 6 -x 4 no intervalo [ - 1,1 ] , por uma parábola, usando os polinômios de Legendre. L n x = 1 2 n . n !d n d x n x 2 - 1 n ; L 0 x = 1 , s
Usando o método dos mínimos quadrados achar a solução aproximada do sistema incompatível: a - 3 b = 0,9 2 a - 5 b = 1,9 - a + 2 b = - 0,9 3 b - b = 3 a + 2 b = 1,1
Um dispositivo tem uma certa característica y que ´e função de uma variável x . Através de várias experiências foi obtido o gráfico:Deseja-se conhecer o valor de y para x=0 , 5 . Da teoria sabe-se que
Determine pelo método dos mínimos quadrados a melhor solução para sistema linear incompatível 2 N + 3 M = 8 N + M = 6 3 N + M = 5 N + 3 M = 12 onde NeM são restritos a valores inteiros.
A resistência à compressão do concreto, σ , decresce com o aumento da razão água/cimento, ω c , (em galões de água por saco de cimento). A resistência à compressão de três amostras de cilindros para v