Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 6IV
Resolver os exercícios 11.1, 11.2, 11.3, 11.4 usando a Regra de Simpson.
Passo 1
Eaí, tudo beleza? Seguindo nosso esqueminha, agora vamos resolver o item IV que é referente ao exercício 11.4, beleza? A regra de Simpson novamente será usada. A mesma em sua forma simples é dada por:
Vamos usá-la para resolver o primeiro exercício (11.4) dado por:
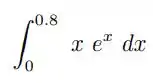
Considerando a tabela:
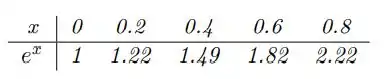
Passo 2
Sabendo que o passo (h) é ficamos com a seguinte fórmula:
Lembrar que temos que multiplicar por .
Agora é só substituir os valores seguindo a tabela:
E com isso finalizamos. Note que o resultado foi apenas um pouco diferente do resultado obtido no exercício 4.
Resposta
O valor da integral foi aproximadamente .
Exercícios de Livros Relacionados
A instrução para a integral ∫ - 2 0 ( x 2 - 1 )d x , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ 0 1 s e nπ td t , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ 1 3 ( 2 x - 1 )d x , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ 0 2 ( t 3 + t )d t , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ 0 π s e ntd t , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.