Exercícios de Regra 1/3 de Simpson - Lista de Exercícios Resolvida
Questão 1
Seja .
Calcule uma aproximação para usando a regra 1/3 de Simpson com . Estime o erro cometido.
Para que valor de teríamos erro inferior a ?
Ver solução completaQuestão 2
Uma criança rolando uma pedra x metros utiliza uma força de 𝑓(𝑥) = 15 + 3𝑠𝑒𝑛(𝑥) dada em Newtons. Sabe-se que o trabalho realizado pela criança para rolar metros é dado por . Determine o número de integrais usando pela fórmula de Simpson com erro de truncamento menor que 0.0004.
Ver solução completaQuestão 3
Calcular a área aproximada limitada por 𝑦 = 𝑙𝑛(𝑥 + 1), 𝑥 = 2, 𝑥 = 3 e 𝑦 = 0, utilizando a fórmula de simpson com o menor número de pontos e erro .
Ver solução completaQuestão 4
Dê um exemplo de uma função onde a regra 1/3 de Simpson calcula o valor exato da integral.
Ver solução completaQuestão 5
Determinar , a distância entre e , para que se possa avaliar com erro inferior a pela regra de Simpson.
Ver solução completaQuestão 6
Usando a regra de Simpson, calcule o valor de com precisão de 4 casas decimais. Compare o resultado com o valor de .
Ver solução completaQuestão 7
Determinar o menor número de pontos necessários para calcular a integral pela regra de simpson com erro inferior a 0,001
Ver solução completaQuestão 8
Use a regra 1/3 de Simpson para integrar a função abaixo entre e com o menor esforço computacional possível (menor número de divisões e maior precisão). Justifique. Trabalhe com três casas decimais.
Ver solução completaQuestão 9
2. Calcule o valor da integral da função abaixo para 8 intervalos utilizando os métodos de Simpson e dos Trapézios. Utilize 3 casas decimais e arredondamento padrão.
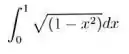
Questão 10
1) Calcule
a) pelo método dos trapézios com e ;
b) pelo método de Romberg usando as 3 estimativas do item (a).
c) Delimite o erro ao se usar o método de Simpsons com e determine a partir disso entre quais valores se encontra a integral exata.
Ver solução completaQuestão 11
3) Uma fórmula de integração aberta não faz uso dos valores da função nos extremos do intervalo. Por exemplo, para calcular dividimos em quatro subintervalos de mesmo tamanho e aproximamos a integral de pela integral do polinômio de grau menor ou igual a 2 que interpola nos pontos interiores 1, 2 e 3.
a) Determine pelo método de diferenças divididas o polinômio que interpola nestes 3 pontos.
b) Integre no intervalo (pela fórmula de Simpson) de maneira a obter a fórmula de integração. Há diferença caso você integre exatamente?
c) Use a fórmula obtida para calcular (sim, uma mudança de variáveis se faz necessária!)
Ver solução completa