Série e Polinômio de Taylor
Teoria
Introdução
Fala meus consagrados, vamos começar a entrar em terras turbulentas e desvendar mistérios que nos fazem até tremer as pernas hehehe já sabe do que eu estou falando?
Já usamos métodos pra achar zero reais de funções, aí passamos pra métodos que transformamos dados em polinômios e até mesmo facilitando a resolução de Integrais.
Mas agora... vamos começar a usar algumas técnicas para resolver Equações Diferenciais Ordinárias... isso mesmo, as temidas EDO’s.
Veja bem, teremos métodos e esquemas numérico pra resolver Problemas de Valor Inicial (PVI) pra encontrar uma função , de modo que teremos algo assim:
Aí, vamos aplicar aquela série famosinha, a tal da série de Taylor para no ponto .
Mas calma, então preciso saber essa tal de série de Taylor primeiro né? Correto!! Por isso, nesse tópico, vamos aprender como usar a série de Taylor, não teremos resoluções de EDO ainda. A série vai ser muuiito importante na frente, temos que entender ela primeiro.
Então, vem tranquilo. O que é série de Taylor?
Cara, basicamente, a série de Taylor é usada para aproximar funções, tipo essa aqui . Vamos ver como ela faz isso já já.
Talvez você tenha visto essa matéria em outra disciplina, e pode estar fresquinho aí na sua cabeça, pode passar isso aqui:
Se você não viu ouuuuuu se já viu, mas não lembra muito bem é uma ótima chance para revisar haha.
O que acontece é que em muitas faculdades Taylor é de fato uma matéria de numérico (pelo menos uma introdução a Taylor) então esse tópico é pra vocês! 
Série de Taylor
Eu aposto que você já ouviu falar alguma coisa sobre essa série, seja em física, EDO, cálculo 3... A série de Taylor é uma série bem famosa, e está por trás de alguns métodos que já vimos em Cálculo Numérico.
Basicamente ela serve para igualar uma função qualquer a uma soma infinita dessa forma:
Onde é a enésima derivada da função no ponto e é a quantidade de termos da nossa série.
Nesse caso dizemos que essa é a Série de Taylor de em torno de . Além disso, toda Série de Taylor tem um “raio de convergência” em torno do ponto onde ela é centrada .
Dentro dessa região a série converge para o valor da função. Fora dessa região, dá tudo errado haha. Em alguns casos, no entanto, e a série aproxima perfeitamente a função em qualquer ponto!
Polinômio de Taylor
Show de bola, mas e daí?
Que raios isso tem a ver com Cálculo Numérico? Hmmm... pensa um pouquinho, aqui em numérico nós estamos seeeeempre tentando fazer algumas aproximações aqui e ali (claro, sempre prezando pra não ter erro né!)
Agora, ao invés de pegarmos a série infinita vamos truncar ela em algum ponto obtendo o polinômio de Taylor de grau .
Dessa maneira, nós podemos aproximar qualquer função por um polinômio! Essa é a graça do Cálculo Numérico, simplificar nossa vida!
É claro que, associado a esse polinômio nós teremos um erro relativo ao truncamento que fizemos. Basicamente, o polinômio de Taylor de grau vai ficar assim:
E o erro de truncamento vai ser dado por:
Naquele mesmo esquema da maioria dos métodos que vimos até agora, onde a raiz é um valor que depende de e se encontra no intervalo entre e . Dificilmente nós iremos calcular esse número, o importante aqui é saber que ele se encontra entre e .
De forma geral o que fazemos é encontrar o máximo de nesse intervalo chegando assim a um limitante do erro cometido:
Obs.: Para obtermos um polinômio de Taylor de grau de alguma função essa função deve ter derivadas até a ordem contínuas.
Exemplo
Então vamos lá! Pra resolver um exercício vamos basicamente calcular alguns polinômios de Taylor .
Bora lá? Vamos calcular o polinômio de Taylor de graus , , e de com .
Como tem todas as derivadas contínuas não precisamos nos preocupar com isso. Calculando as derivadas de primeira até quarta, temos que:
Aplicando na função e em todas as derivadas, ficamos com:
Beleza, até aí tranquilo. Agora vamos relembrar aquela fórmula que vimos lá encima:
Com isso vamos calcular os polinômios com .
Para :
:
:
:
Tudo beleza? Olha essa imagem pra ver como à medida que aumentamos o nossa aproximação vai melhorando:
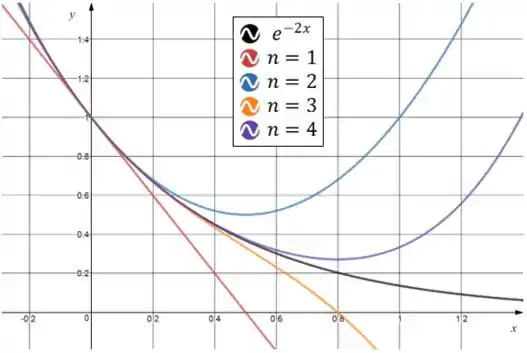
Olhando o gráfico, percebemos que todas as aproximações tem valor exato em 0, mas isso acontece devido ao fato de que nosso polinômio de Taylor foi construído em torno de .
Vamos ver o erro de cada uma? O erro é dado por:
Para :
Para :
Para :
Para :
Com isso, podemos ver em todos os limitantes que, conforme vai se afastando de , o erro vai aumentando. Isso porque os erros são dados em função de ! Mas vimos agora que quanto maior o melhor são as aproximações em torno de .
Para valores distantes de os maiores não serão necessariamente melhores!
E é só isso que eu tinha pra falar mesmo galera! Vamos fazer uns exercícios que no próximo tópico veremos uma aplicação desse polinômio de Taylor.
Série de Taylor
Polinômio de Taylor
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Lista de Exercícios sobre Sequências e Séries – UFSCAR – Questão 20
Encontre a série de Taylor de em torno de :
Passo 1
Lembrando que a série de Taylor é definida por:
Em torno de temos:
O que temos que fazer agora é tentar achar um padrão no valor das derivadas de .
Passo 2
Vamos montar uma tabelinha para as derivadas de e seus valores no ponto :
Por essa tabela conseguimos perceber o seguinte padrão: só os termos de ímpar vão aparecer na série pois os de par são sempre zero. E os componentes de termo ímpar vão trocando de sinal!
Podemos substituir todos os na fórmula por para pegarmos apenas os ímpares. E usando o termo para cuidar da troca de sinal ficamos com:
Prontinho!! Essa é a nossa série de Taylor!
Resposta
Exercício Resolvido #2
Lista 0 – Professora Juliana – UFRJ – Questão 1
Encontre a série de Taylor em torno de para as funções:
Passo 1
Lembrando que a série de Taylor é definida por:
Em torno de temos:
O que temos que fazer agora é tentar achar um padrão no valor das derivadas de cada . Vai ficar mais claro quando vocês verem sendo feito haha.
Passo 2
Vamos começar escrevendo o valor de algumas derivadas de :
Por essa tabela conseguimos pegar o seguinte padrão, só os termos de ímpar vão aparecer na série pois os de par são sempre zero. E os componentes de termo ímpar vão trocando de sinal!
Podemos substituir todos os na fórmula por para pegarmos apenas os ímpares. E usando o termo para cuidar da troca de sinal ficamos com:
Passo 3
Essa provavelmente vai ficar bem parecida com a do seno né? Fazendo a mesma tabelinha:
O padrão é praticamente o mesmo, mas dessa vez temos apenas os pares! Então vamos trocar por pra pegar só os pares e manter o termo pra troca de sinais.
Passo 4
Montamos a tabelinha de novo:
E aí, essa tabela ta te lembrando alguma coisa? Pra mim ela ta igualzinha ao fatorial de né? Então nossa série vai ficar:
Passo 5
Precisa nem de tabela pra dizer o que vai acontecer aqui né? Independente do , vai valer sempre . Logo, a série de Taylor vai ficar:
Passo 6
Esse não ta tão óbvio quanto o último né? Vamos para a nossa tabelinha de novo:
Vamos passo a passo. Repara como os termos estão trocando de sinal sempre que mudamos o ! E que para ímpar o sinal é positivo. Logo, teremos um termo na nossa série de Taylor.
Outra coisa importante é que temos de novo aquela cara de fatorial! Só que agora para apareceu o fatorial de . Então tem que ter um na jogada.
Dessa forma, nossa expressão genérica para deve ser
Essa fórmula só não bate com o resultado de , mas como para esse temos nem precisamos contar ele! Nossa série de Taylor ficaria então:
Repare que começamos em ao invés de justamente para eliminar aquela primeira linha da tabela. Outro detalhe importante é que podemos decompor em
Assim ficamos com:
É comum iniciarmos a série com , para isso basta trocarmos os por :
Ufa, esse é o valor final da nossa série de Taylor!
Resposta
Exercício Resolvido #3
Elaboração Própria
Encontre , usando série de Taylor gerada por em , sabendo que:
Passo 1
Lembrando que a série de Taylor é definida por:
Como todos os valores das derivadas da função estão em torno de , vamos fazer a série com . Em torno de temos:
O que temos que fazer agora é substituir os valores da tabela e achar o polinômio correspondente.
Passo 2
A tabela é:
Por essa tabela conseguimos montar o polinômio aplicando os valores na fórmula de Taylor:
Prontinho!! Esse é o nosso polinômio!
Resposta
Exercício Resolvido #4
Elaboração Própria
Encontre , usando série de Taylor gerada por em , sabendo que:
Passo 1
Lembrando que a série de Taylor é definida por:
Como todos os valores das derivadas da função estão em torno de , vamos fazer a série com . Em torno de temos:
O que temos que fazer agora é substituir os valores da tabela e achar o polinômio correspondente.
Passo 2
A tabela é:
Por essa tabela conseguimos montar o polinômio aplicando os valores na fórmula de Taylor:
Prontinho!! Esse é o nosso polinômio!
Resposta
Exercício Resolvido #5
Elaboração Própria
Encontre , usando série de Taylor gerada por em , sabendo que:
Passo 1
Lembrando que a série de Taylor é definida por:
Como todos os valores das derivadas da função estão em torno de , vamos fazer a série com . Em torno de temos:
O que temos que fazer agora é substituir os valores da tabela e achar o polinômio correspondente.
Passo 2
A tabela é:
Por essa tabela conseguimos montar o polinômio aplicando os valores na fórmula de Taylor:
Prontinho!! Esse é o nosso polinômio!
Resposta
Exercício Resolvido #6
Lista de Exercícios sobre Sequências e Séries – UFSCAR – Questão 18
Mostre que a função pode ser representado como série de Taylor em torno de para todo
Passo 1
Lembrando que a série de Taylor é definida por:
Em torno de temos:
O que temos que fazer agora é tentar achar um padrão no valor das derivadas de .
Passo 2
Vamos montar uma tabelinha para as derivadas de e seus valores no ponto :
Por essa tabela conseguimos perceber o seguinte padrão: só os termos de par vão aparecer na série pois os de ímpar são sempre zero. E os componentes de termo par vão trocando de sinal!
Podemos substituir todos os na fórmula por para pegarmos apenas os pares. E usando o termo para cuidar da troca de sinal ficamos com:
Prontinho!! Essa é a nossa série de Taylor!
E perceba que ela não possui restrições, portanto é definida para qualquer .
Resposta
Exercício Resolvido #7
Lista 0 – Professora Juliana – UFRJ – Questão 15
Encontre a série de taylor de em .
Passo 1
Tem duas maneiras de resolvermos essa.
A primeira é na marra encontrando um padrão na derivada de ordem . O problema é que nesse caso esse padrão pode ser meio complicado de se achar haha.
A segunda forma requer um pulo do gato meio sacana. No último exercício nós vimos que a série de é a seguinte:
E o que aconteceria se a gente substituísse por ? Ficaria assim né:
E é essa aí a resposta! Não esperava por essa né? Pois é, muitas funções complicadas podem ter sua série deduzida usando como base funções mais simples com séries conhecidas!
Resposta
Exercício Resolvido #8
Lista 0 – Professor Daniel – UFRJ – Questão 1
Obtenha as aproximações linear e quadrática para , em torno de usando a fórmula de Taylor.
Em um mesmo gráfico, esboce a curva e as aproximações linear e quadrática obtidas em . Através do gráfico analise o comportamento das aproximações constando que representam apenas localmente. Qual das duas curvas você escolheria para aproximar em torno de .
Obs.: Os gráficos podem ser esboçados a mão ou traçados usando software ou ainda na calculadora.
Passo 1
Nessa letra ele quer simplesmente os polinômios de Taylor de graus e . Temos:
, :
, :
Passo 2
O próximo passo é esboçar o gráfico disso. Fica assim oh:
Como era de se esperar todas as aproximações têm o valor exato em . A curva azul é o polinômio de Taylor de grau e a curva vermelha é o polinômio de Taylor de grau .
Outra conclusão que chegamos por meio desse gráfico é que em torno de , o polinômio de Taylor de grau é uma aproximação melhor que o de grau .
Resposta
:
:
Todas as aproximações têm o valor exato em . Em torno de , o polinômio de Taylor de grau é uma aproximação melhor que o de grau .
Exercício Resolvido #9
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 15, exercício 7
Seja .
Encontre o polinômio de Taylor de grau em torno de .
Encontre um limitante para o erro e o erro exato de .
Repita o item usando .
Repita o item usando o polinômio do item .
Passo 1
Temos:
Encontrando o polinômio com , :
Que resultado bunda haha. Nosso polinômio é .
Passo 2
Um limitante para o erro é:
Nesse caso,
E o erro exato foi de:
Ou seja, o erro coincidiu com nosso limitante do erro.
Passo 3
Agora queremos o polinômio para o caso onde , :
Passo 4
O limitante para o erro é dado por:
Nesse caso,
Como só nos interessamos pelo módulo:
E o erro exato foi de:
Acabou dando o mesmo erro haha. De novo coincidindo com o limitante.
Resposta
Exercício Resolvido #10
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 16, exercício 15
Use um polinômio de Taylor em torno de para aproximar com uma acurácia de .
Passo 1
Se liga numa coisa. Aqui o cara não deu o grau do polinômio de Taylor pra gente! Por que será?
Porque ele quer que a gente descubra, é claro! E como ele definiu o erro máximo, vamos usar nossa fórmula
Nesse caso,
Logo,
Agora vem a parte mais chata. Sabemos que nossa pode ser um seno ou um cosseno dependendo de ser par ou ímpar.
Se for par, então será um seno e a derivada terá como módulo do valor máximo:
Se for ímpar, então será um cosseno e a derivada terá como módulo do valor máximo:
A solução mais rápida seria simplesmente considerar o máximo geral como o máximo desses dois valores. No caso, . Substituindo:
Resolver isso aí ta fora de questão né? Vamos jogar uns valores de e ver no que dá:
:
:
:
Opa, achamos um limitante inferior à . Logo, queremos o polinômio de Taylor de grau !
Passo 2
Calculando as derivadas de :
Substituindo na fórmula:
Substituindo na fórmula:
Se compararmos com o valor real de teremos um erro de: