Método de Euler
Produzido por Bruno PestanaTeoria
Introdução às EDO’s
Falaaaaa meus caros, espero que esteja tudo numa boa aí! Eu to mega feli, agora vamos começar um assuntinho que estamos prorrogando desde o início desse capítulo. CHEGOU A HORA DE RESOLVER EDO ATÉ SER O NINJA DAS EDO´S. Vamos sair desse tópico sabendo achar , se:

Eu não sei se você ta animado, mas eu estou!
Talvez você, meu jovem aprendiz, já tenha alguma noção da tal da Equação Diferencial e Ordinária, que carinhosamente chamamos de EDO. Mas, se é a primeira vez que você ouvir falar dela, nem se estresse, nós vamos explicar tudo tin tin por tin tin.
Uma EDO geralmente é uma equação com essa carinha aqui:
Ou com essa:
Então, o que essa equação tem de tão especial? Uma EDO é uma equação que envolve uma função, suas derivadas, e uma variável independente. Nesse caso, temos uma em função de uma variável independente e a derivada dessa função, que é . Uma observação é que essas letras podem mudar sem problemas, ok? Podemos ter uma função de uma variável , por exemplo. São apenas letras, só precisamos identificar cada uma!
Como identificar? A função possui uma derivada, a variável, não. 😉
E uma coisa que devemos saber sobre as EDO´s é que elas tem uma ordem. Basicamente, a ordem tem a ver com a maior derivada que aparece na nossa equação. Então, olhando os exemplos alí de cima vemos que a primeira EDO é de ordem 2 (a máxima derivada é de ordem 2) e a segunda de ordem 1. SHOOOW DE BOLA!
Lá vem o PVI
E um PVI? Dei uma retocada nele láaaa quando eu falei sobre os polinômios de Taylor. Só que agora vamos ver com mais carinho e atenção, já que ele será o foco do nosso estudo.
Afinal, o que é um PVI, Problema de Valor Inicial?
Calma meu jovem, não coloque a carroça na frente dos bois. Antes de falar o que é um PVI, vamos entender porque eles são tão comuns. Veja essa EDO:
Resolver uma EDO é achar todas as funções que satisfazem à equação. Nesse caso, a solução é:
Onde e são constantes reais arbitrárias. Isto é, pra qualquer valores que a gente jogar nessas constantes, a função sempre vai satisfazer à EDO. Chamamos isso de solução geral da EDO. Pra determinar uma função só, precisamos impor mais umas condições:
Agora sim temos só uma solução! Vimos que a geral é:
Então, precisamos achar os valores de e . Para isso, vamos substituir os pontos que foram dados:
Onde . Fazendo e , achamos os valores para e , que são:
Dessa forma, a resposta da EDO será:
Isso aí é um PVI : a EDO mais os valores iniciais da função e de suas derivadas. Observe que para a nossa EDO aqui, que é de ordem , temos condições iniciais, sobre e . Se fosse de ordem , precisaríamos só do valor de pra determinar a solução.
O Teorema da Existência e Unicidade nos diz que, para qualquer PVI de ordem , ou seja, onde temos uma EDO de ordem e também condições iniciais, obtemos sempre uma única solução.
Dessa forma, o PVI serve para quando o valor da função e suas derivadas são especificados no mesmo ponto (para o mesmo valor da variável independente, );
Entra o Cálculo Numérico
Até agora nós só generalizamos EDO, afinal, existem disciplinas que falam só delas ! Então, vamos trazer uma abordagem que vai te fazer desbravar essas terras desconhecidas. Bora lá?

Pra ajudar, as vezes nessas disciplinas você aprende a resolver um número limitado de EDO´s, geralmente só as bonitinhas, ou tipo essa aqui:
Só que, o cálculo numérico vai te ensinar a resolver qualquer tipo de EDO, e pasme, vamos fazer isso do jeito que sabemos fazer melhor.... APROXIMA TUDOOOOO.
E, para variar, teremos nossos limites, que serão os critérios de parada.
A abordagem mais tranquila para estimar uma inclinação é usar a equação diferencial para obter uma estimativa na forma da primeira derivada em .
Então temos o Método de Euler, ele serve para resolver Problemas de Valor Inicial de primeira ordem, então ele é bem tranquilinho. Já que você deve conhecer só os palpites e valores iniciais e a equação vai ter no máaaaaximo derivadas de ordem um .
Veja bem, a lógica é tranquilona. Suponha que queremos saber valores da função definida pelo seguinte PVI:
Nesse intervalo nós conhecemos o intervalo . Aqui vai uma observação que talvez demore um pouco pra você entender, talvez só depois de você ver a parte de Equações de Ordem Superior, então se parecer meio nada a ver agora, não se preocupe e siga em frente: o pode ser um vetor de funções! Nesse caso as fórmulas são as mesmas, só vamos ter mais contas na hora de resolver os exercícios.
Talvez você se confunda em achar o na hora de resolver o exercício, mas saca só. Na EDO:
O vai ser:
Viu o que aconteceu? Nós escrevemos a derivada em função do .
OBS.: Repare que pode ser em função de , de ou qualquer outra variável, isso vai depender do problema!
Voltando a descrição do método, vemos que, sabendo o valor de em um ponto podemos calcular a sua derivada. Mas aqui fazemos o pulo do gato: vamos calcular os valores de em um número finito de pontos , todos eles espaçados por um passo , onde . Nesse caso podemos escrever a derivada como:
Só que quando temos um intervalo muuuuito pequeno, no caso tendendo a , ele pode ser aproximado pelo nosso passo , já que é o intervalo entre um ponto e outro também. O grande lance é que tentamos deixar esse passo o menor possível para aumentar a precisão, logo quando tende a , ele vira nosso . Com isso:
Logo, escrevendo , e sabendo que . Vemos que:
Essa é a fórmula do Método de Euler. É uma recursão, onde achamos em função de .
A questão vai te dar o , o e o . Daí, amigo, é só fazer conta. As aproximações seguem da seguinte forma:
Então, se tivéssemos:
E quiséssemos estimar , com , faríamos:
Para chegar em , partindo de a um passo , precisamos fazer duas iterações apenas. Pois de para , é uma iteração e de para é uma outra iteração. Então, nosso objetivo é achar o .
Além disso, já vimos que:
Pela fórmula de recorrência:
Para achar o :
Calculando o :
E esse é o nosso resultado para . 😊 Viu? Falei que você ia sair daqui sabendo resolver esse problema hehe.
Então, repare que se escolhêssemos um passo menor, faríamos mais iterações, já que demoraria mais para sair de para , e quanto mais iterações, mais próximos chegamos do valor real. Por isso, quanto menor o passo , mais preciso é o nosso resultado.
Algoritmo
Como a graça do cálculo numérico é aprender os métodos para que um computador calcule, se quiser implementar o Método de Euler no computador o algoritmo vai ser mais ou menos assim:
- Defina o passo
- Defina o intervalo em que vamos estimar :
- Pegamos um vetor onde vamos guardar os valores de e fazemos .
- Pra entre e fazemos
Vamos fazer uns exercícios pra você manjar tudo sobre o Método de Euler e arrasar na sua prova!
Lá vem o PVI
Entra o Cálculo Numérico
Algoritmo
Exercícios Resolvidos
Exercício Resolvido #1
Ruggiero, M. A. e Lopes, V. L. R. Cálculo Numérico: aspectos teóricos e computacionais. 2 ed.São Paulo: Pearson Makron Books, 1996. Cápitulo 8. Exercício 15. (Adaptado)
Calcule para utilizando Euler com . Compare seus resultados com os valores exatos de nos pontos , sabendo que =
Passo 1
Temos essa EDO para analisar:
Onde:
e . E queremos .
Aqui vamos usar Euler de passo . Vamos montar uma tabelinha com os :
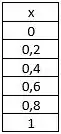
Logo, pela tabela, podemos encontrar uma relação entre . Percebemos que podemos escrever o seguinte:
Isso, porque os valores de são apenas múltiplos de .
Lembramos da fórmula de recorrência:
Nesse caso temos:
Passo 2
A fórmula de recorrência fica:
Substituindo :
Daí ficamos com:
E, aplicando sucessivamente a recorrência para os outros valores de , vamos obter:
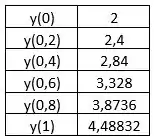
Agora, vamos comparar com os valores reais da função = :
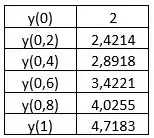
Logo o calculado é . Veja que os valores Método de Euler crescem mais devagar que os reais
Resposta
Exercício Resolvido #2
Ruggiero, M. A. e Lopes, V. L. R. Cálculo Numérico: aspectos teóricos e computacionais. 2 ed.São Paulo: Pearson Makron Books, 1996. Capítulo 8. Exercício 16. (Adaptado)
Considere o PVI:
Calcule aproximações para , usando o método de Euler com e :
Passo 1
Aqui vamos nós. Nessa questão está pedindo para calcular usar Euler com as seguintes configurações
e
Passo 2
Vamos tentar generalizar as coisas antes, já que estamos lidando com dois passos diferentes. Se liga:
Ou seja, um dado ponto é obtido através de vezes o valor do passo. Essa expressão é válida para qualquer passo.
Temos que :
A fórmula de recorrência fica:
Mas pera aí:
Logo:
Do mesmo jeito teremos podemos calcular :
Percebeu o que está acontecendo? Calculamos ,ee todos deram 1. Se quiséssemos calcular como o resultado seria o mesmo! Já que o termo depende do anterior podemos concluir que se trata de uma função constante!!
Normalmente, para resolver esse tipo de questão, o natural seria continuar o processo até que um que fosse referente ao ponto que é o que deseja avaliar.
Para o passo teríamos que ir até o , pois para teríamos:
Para o passo h=0,25, teríamos que ir até o , pois para , teríamos:
Mas que como nesse caso, todos os y darão o mesmo valor, a aproximação y será igual a, não importando o passo, pois o Método de Euler devolve uma função constante.
Legal né?(:
Resposta
em ambos os casos
Exercício Resolvido #3
Ruggiero, M. A. e Lopes, V. L. R. Cálculo Numérico: aspectos teóricos e computacionais. 2 ed.São Paulo: Pearson Makron Books, 1996. Cápitulo 8. Exercício 17. (Adaptado)
Considere o PVI:
Encontre a solução aproximada usando o método de Euler com e , considerando
Passo 1
Aqui vamos usar Euler com as seguintes configurações
e
Passo 2
A fórmula de recorrência fica:
Para :
Daí:
E sucessivamente obtemos:

Passo 3
Para
Daí:
E sucessivamente, obtemos:
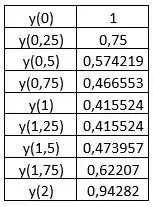
Veja que obtemos uma diferença bastante significativa diminuindo o passo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Lista de exercícios - FEI
Dada a equação diferencial calcule 𝑇(2) e 𝑇(3) com 3 casas decimais, usando o método de Euler. Para t=1, temos T=3. Escrever as fórmulas adaptadas à questão.
Passo 1
Bom o professor já entregou pra gente a EDO separadinha do lado direito da igualdade e a derivada do lado esquerdo. Então o que a gente precisa agora é escrever a equação do Método de Euler adaptadas ao problema.
Show de bolinhas, vai ser tranquilo de resolver esse negócio!!
Passo 2
Bom a gente sabe que quando , temos . Então substituindo esses valores na equação que acabamos de encontrar, olha como fica.
Aeeeew, já temos metade da questão . Agora é só repetir o mesmo processo para obter o
Sabemos que quando , temos
Resposta
Exercício Resolvido #5
Lista de exercícios - FEI
Um indivíduo está recebendo uma injeção intravenosa de glicose na taxa constante de . É um fato biológico que, dentro de certos limites, o corpo utiliza a glicose em uma taxa proporcional à sua concentração na corrente sanguínea. A EDO que modela esta situação é: , onde é o volume de sangue no corpo do indivíduo, consideraremos que a quantidade de glicose injetada não altera V apreciavelmente. A mudança da concentração de glicose no sangue é o resultado de dois fatores: um aumento devido à injeção intravenosa permanente e a redução devida à retirada da glicose sanguínea pelo corpo. Em um tempo t qualquer, a taxa de mudança de concentração devida à injeção intravenosa permanente é , e a taxa de mudança de concentração devida aos processos metabólicos é −𝑘𝑦, para alguma constante positiva. Supondo , e , como calcular, pelo método de Euler, a concentração de glicose entre 10 e 14 minutos com 𝑒 ?
Passo 1
A EDO já tá separadinha pra gente, do lado direito da igualdade e a derivada do lado esquerdo. Então o que a gente precisa agora é escrever a equação do Método de Euler adaptadas ao problema. Bora substituir as constantes que o professor deu!
A fórmula de Euler geral é essa aqui:
Nós sabemos que o passo e pra esse problema, então substituindo na fórmula geral, vamos ter:
Show de bolinhas, vai ser tranquilo de resolver esse negócio!!
Passo 2
Bom a gente sabe que quando , temos . Então substituindo esses valores na equação que acabamos de encontrar, olha como fica.
Então sabemos agora que quando , temos . Com esses dados já podemos encontrar , é só aplicar novamente a equação adaptada, bora lá.
Bora achar o próximo,
Tamo quase no final, falta achar agora somente o .
Resposta
Exercício Resolvido #6
Lista de exercícios - FEI
Calcular a EDO no intervalo , para e passo . Resolver pelo método de Euler.
Passo 1
Falaaaa! td certinho?
Nessas questões a primeira coisa que você precisa é escrever a equação do Método de Euler adaptada ao problema. Então vamos a ela!!
Esse na fórmula, é tudo que estiver do lado direito da igualdade, separado de . Pra esse exercício fica assim...
Show de bolinhas, vai ser tranquilo de resolver esse negócio!!
Passo 2
Bom a gente sabe que quando , temos . É isso que ele quer dizer com esse .
Então substituindo esses valores na equação que acabamos de encontrar, olha como fica.
Metade da nossa questão ta garantida, já temos o . Agora é só repetir o mesmo processo para obter o .
Sabemos que quando , temos