Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Critério para Possuir Inversa de Funções Vetoriais

Ver Todos os Exercícios

Teoria

O que é?

O que significa dizer que uma função é a inversa da outra?

Bom, se a gente tem uma função F que leva elementos de um conjunto A num conjunto B , a inversa dessa função é uma função que faz o caminho inverso, ou seja, que leva os elementos do conjunto B pro conjunto A .

Isso faz bastante sentido né?

Então, colocando termos matemáticos na parada, podemos dizer que se F tem domíno A e imagem B , então a sua inversa F - 1 tem domínio em B e imagem em A .

Ou seja, o domínio vira imagem e a imagem vira domínio!

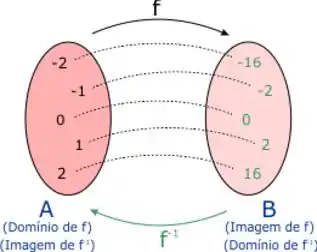
Guarda isso na sua cabeça:

Imagem de F = Domínio de F - 1

Até ai tranquilo, né?

Agora, todas as funções do universo possuem inversa? Como a gente vai saber se uma função possui inversa ou não?

Vou te dizer isso agora!

Critério para possuir inversa

Bom, pra te explicar essa parte, vou dividir nossas funções em duas categorias:

  1. Função Afim
  2. Função vetorial de várias variáveis

E no final te mostrar que os critérios para essas duas categorias dependem basicamente de uma mesma condição.

Vamos lá!

  1. Função Afim

    2. Uma função afim T é uma função que pode ser escrita na forma

    T X = A . X - X 0 + Y 0

    Onde X ,   X 0 ,   Y 0 representam vetores, com quantas componentes se desejar e A representa a matriz de coeficientes. Assim

    T x , y = 2 0 1 4 x + 1 y - 2   + 5 6

    Nesse caso:

    A = 2 0 1 4

    X = x y

    X 0 = - 1 2

    Y 0 = 5 6

    E os vetores tem 2 componentes.

    Tá, mas i ae, quando essa função vai ser inversível?

    Quando a matriz de coeficientes A for inversível.

    E você se lembra quando uma matriz é inversível?

    Não?

    A gente aprende isso lá em Álgebra, mas não tem problema, porque eu vou te lembrar aqui também:

    Uma matriz é inversível quando seu determinante é diferente de zero.

    No caso da nossa matriz A temos:

    det ⁡ A = 2 0 1 4 = 2.4 - 0.1 = 8 ≠ 0  

    Portanto, nossa função afim tem inversa!

  2. Função vetorial de várias variáveis

Uma função vetorial de várias variáveis

F X = Y

Onde X e Y são vetores de quantas componentes se queira.

Por exemplo

F x , y , z = ( x + 1 , z + y , z )

É inversível nas proximidades de um ponto X 0 se sua matriz jacobiana for inversível nesse ponto.

OI?!

Calma, é fácil!

Matriz jacobiana eu já te disse o que é: é a matriz das derivadas da nossa função vetorial, onde as colunas são formadas pelas derivadas parciais das funções componentes em relação a cada um dos parâmetros:

J F = ∂ f 1 ∂ x ∂ f 1 ∂ y ∂ f 1 ∂ z ∂ f 2 ∂ x ∂ f 2 ∂ y ∂ f 2 ∂ z ∂ f 3 ∂ x ∂ f 3 ∂ y ∂ f 3 ∂ z = 1 0 0 0 1 1 0 0 1

E para uma matriz ser inversivel num ponto, você acabou de se lembrar que seu determinante tem que ser diferente de zero.

Assim, se a gente quiser saber se nossa função F é inversivel perto do ponto X 0 = ( 1,1 , 1 ) , basta substituir na matriz jacobiana e verificar se o determinante é diferente de zero.

J F X 0 = 1 0 0 0 1 1 0 0 1

det ⁡ J F X 0 = 1 0 0 0 1 1 0 0 1 = 1.1 . 1 + 0 . 1 . 0 + 0 . 1 . 1 - 0 . 1 . 0 - 1 . 1.0 - 0.0 . 1 = 1 ≠ 0

Portanto, nossa função vetorial tem inversa!

E é só isso, simples assim!

No final das contas, pra saber se uma função tem inversa tudo o que você deve verificar é:

  • Para função afim: Se o determinante da matriz de coeficientes A é diferente de zero.
  • Para funções vetoriais: Se o determinante da matriz de derivadas num ponto X 0 é diferente de zero

Critério para possuir inversa

Exercícios Resolvidos

Exercício Resolvido #1

UFF, Cálculo 2B, Parte 13, exemplo 13.1.1, item a.

Considere a função T : R 3 → R ³ definida por:

T x , y , z = 4 0 5 0 1 - 6 3 0 4 x - 1 y z - 1 + 1 5 2

Mostre que T é inversível.

Passo 1

Bem, o que a gente tem ai é uma função afim

T X = A . X - X 0 + Y 0

Onde

A = 4 0 5 0 1 - 6 3 0 4

X = x y z

X 0 = 1 0 1

Y 0 = 1 5 2

E , para ser inversivel, o determinante da matriz de coeficientes A tem que ser diferente de zero.

Passo 2

-

Vamos calcular esse determinante:

det ⁡ A = 4 0 5 0 1 - 6 3 0 4 = 4.1 . 4 + 0 . - 6 . 3 + 5.0 . 0 - 5.1 . 3 - 4 . - 6 . 0 - 0.0 . 4 = 1 ≠ 0

Portanto, como esse determinante é diferente de zero, nossa função afim é inversivel.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2004, p.324. questão 4.

Se u , v = F x , y = ( e x cos ⁡ y , e x sen ⁡ y ) para que pontos ( x 0 , y 0 ) a função F tem inversa definida numa bola aberta de centro do ponto F ( x 0 , y 0 ) ?

Passo 1

Pra saber se a função vetorial tem inversa nas proximidades do ponto ( x 0 , y 0 ) , o determinante da matriz jacobiana nesse ponto, tem que ser diferente de zero.

Aqui a gente precisa saber qual, ou quais, são esses pontos, que fazem esse determinante ser diferente de zero.

Passo 2

Vamos começar calculando o jacobiano:

J F = ∂ f 1 ∂ x ∂ f 1 ∂ y ∂ f 2 ∂ x ∂ f 2 ∂ y = e x cos ⁡ y - e x sen ⁡ y e x sen ⁡ y e x cos ⁡ y

No ponto ( x 0 , y 0 ) :

J F ( x 0 , y 0 ) = e x 0 cos ⁡ y 0 - e x 0 sen ⁡ y 0 e x 0 sen ⁡ y 0 e x 0 cos ⁡ y 0

Passo 3

Agora vamos calcular o determinante:

det ⁡ J F x 0 , y 0 = e x 0 cos ⁡ y 0 - e x 0 sen ⁡ y 0 e x 0 sen ⁡ y 0 e x 0 cos ⁡ y 0 = e 2 x 0 c o s 2 y 0 + e 2 x 0 s e n 2 y 0 = e 2 x 0

Passo 4

Por fim, precisamos saber para que valores de ( x 0 , y 0 ) esse determinante é diferente de zero.

det ⁡ J F x 0 , y 0 ≠ 0

e 2 x 0 ≠ 0

Isso é diferente de zero para qualquer valor de x 0 , certo?

Agora, e os valores de y 0 ?

Bom, a expressão do determinante sequer depende de y 0 . Isso significa que y 0 pode assumir qualquer valor.

Logo, a função F tem inversa para todos os pontos

x 0 , y 0 ∈ R ²

Resposta

A função F tem inversa para todos os pontos

x 0 , y 0 ∈ R ²

Exercício Resolvido #3

UFF, Cálculo 2B, Listas, Lista 12, questão 6.

A função f ρ , θ , ϕ = ρ cos ⁡ θ sen ⁡ ϕ , ρ sen ⁡ θ sen ⁡ ϕ , ρ cos ⁡ ϕ está definida para todo ρ , θ , ϕ ∈ R ³ . Em que pontos ρ 0 , θ 0 , ϕ 0 ∈ R ³ é possível garantir que essa função admite inversa numa vizinhança do ponto ρ 0 , θ 0 , ϕ 0 ?

Passo 1

Pra saber se a função vetorial tem inversa nas proximidades do ponto ρ 0 , θ 0 , ϕ 0 , o determinante da matriz jacobiana nesse ponto, tem que ser diferente de zero.

Aqui a gente precisa saber qual, ou quais, são esses pontos, que fazem esse determinante ser diferente de zero.

Passo 2

Vamos começar calculando o jacobiano:

J F = ∂ f 1 ∂ ρ ∂ f 1 ∂ θ ∂ f 1 ∂ ϕ ∂ f 2 ∂ ρ ∂ f 2 ∂ θ ∂ f 2 ∂ ϕ ∂ f 3 ∂ ρ ∂ f 3 ∂ θ ∂ f 3 ∂ ϕ = cos ⁡ θ sen ⁡ ϕ - ρ sen ⁡ θ sen ⁡ ϕ ρ cos ⁡ θ cos ⁡ ϕ sen ⁡ θ sen ⁡ ϕ ρ cos ⁡ θ sen ⁡ ϕ ρ sen ⁡ θ cos ⁡ ϕ cos ⁡ ϕ 0 - ρ sen ⁡ ϕ

No ponto ρ 0 , θ 0 , ϕ 0 :

J F ρ 0 , θ 0 , ϕ 0 = cos ⁡ θ 0 sen ⁡ ϕ 0 - ρ 0 sen ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 cos ⁡ θ 0 cos ⁡ ϕ 0 sen ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 cos ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 sen ⁡ θ 0 cos ⁡ ϕ 0 cos ⁡ ϕ 0 0 - ρ 0 sen ⁡ ϕ 0

Passo 3

Agora vamos calcular o determinante:

det ⁡ J F ρ 0 , θ 0 , ϕ 0 = cos ⁡ θ 0 sen ⁡ ϕ 0 - ρ 0 sen ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 cos ⁡ θ 0 cos ⁡ ϕ 0 sen ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 cos ⁡ θ 0 sen ⁡ ϕ 0 ρ 0 sen ⁡ θ 0 cos ⁡ ϕ 0 cos ⁡ ϕ 0 0 - ρ 0 sen ⁡ ϕ 0 =

- ρ 0 2 c o s 2 θ 0 s e n 3 ϕ 0 - ρ 0 2 sen 2 ⁡ θ 0 sen ⁡ ϕ 0 c o s 2 ϕ 0 + 0 - ρ 0 2 cos 2 ⁡ θ 0 cos 2 ⁡ ϕ 0 sen ⁡ ϕ 0 - 0 - ρ 0 ² sen ² ⁡ θ 0 sen ³ ⁡ ϕ 0  

= - ρ 0 2 s e n 3 ϕ 0 c o s 2 θ 0 + sen 2 ⁡ θ 0 - ρ 0 2 sen ⁡ ϕ 0 c o s 2 ϕ 0 sen 2 ⁡ θ 0 + cos 2 ⁡ θ 0 =

- ρ 0 2 s e n 3 ϕ 0 - ρ 0 2 sen ⁡ ϕ 0 c o s 2 ϕ 0 = - ρ 0 2 sen ⁡ ϕ 0 s e n 2 ϕ 0 + c o s 2 ϕ 0 =

- ρ 0 2 sen ⁡ ϕ 0

Passo 4

Por fim, precisamos saber para que valores de ρ 0 , θ 0 , ϕ 0 esse determinante é diferente de zero.

det ⁡ J F ρ 0 , θ 0 , ϕ 0 ≠ 0

ρ 0 2 sen ⁡ ϕ 0 ≠ 0

Para isso ser diferente de zero, temos que:

ρ 0 2 ≠ 0

ρ 0 ≠ 0

E

sen ⁡ ϕ 0 ≠ 0

ϕ 0 ≠ k π

E o θ ?

Nossa expressão para o determinante sequer depende de θ 0 . Isso significa que θ 0 pode assumir qualquer valor.

Logo, a função f tem inversa para todos os pontos

{ ρ 0 , θ 0 , ϕ 0 ∈ R 3 ; ρ 0 ≠ 0   e   ϕ 0 ≠ k π }

Resposta

A função f tem inversa para todos os pontos

{ ρ 0 , θ 0 , ϕ 0 ∈ R 3 ; ρ 0 ≠ 0   e   ϕ 0 ≠ k π }