Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teorema de Gauss

Ver Todos os Exercícios

Teoria

Introdução

O Teorema de Gauss, também conhecido como Teorema da Divergência, relaciona uma integral tripla sobre um volume W com uma integral de superfície sobre a sua fronteira, que chamamos de ∂ W . Você vai perceber que esse teorema possui certa semelhança com os teoremas de Stokes e Green.

Para aprender a aplicar o Teorema de Gauss, você precisa ter dois conceitos em mente. Primeiro, temos que saber como orientar essa superfície ∂ W que limita o sólido W . Você já viu que uma superfície é orientada por um campo vetorial n → de vetores normais a ela, mas há dois possíveis, qual escolhemos? Para uma superfície que limita um sólido estar orientada positivamente, seu vetor normal deve sempre apontar para fora do sólido. Veja a figura abaixo:

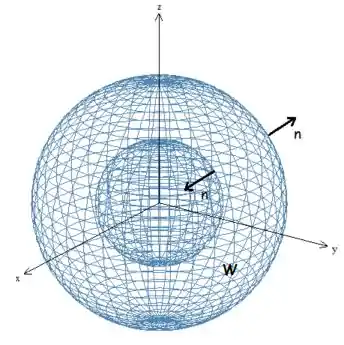
A região W está compreendida entre duas esferas de raios diferentes. Como você pode ver, n →   sempre aponta para fora de W .

Agora precisamos introduzir outro conceito: o divergente de um campo vetorial. Para isso, considere um campo F → ( x , y , z ) = ( F 1 ,   F 2 ,   F 3 ) que tenha derivadas parciais definidas no R 3 . Sendo assim, seu divergente é dado por:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

Podemos obter essa expressão fazendo o produto escalar:

d i v F → = ∇ ⋅ F →

Onde ∇ é o operador de derivadas parciais:

∇ = ∂ ∂ x ,   ∂ ∂ y ,   ∂ ∂ z

Observação: Não confunda divergente com rotacional! O divergente é obtido por um produto escalar com o operador ∇ , o que resulta em um número, enquanto o rotacional é obtido por um produto vetorial, o que resulta em um vetor.

O Teorema de Gauss

Sendo ∂ W uma superfície orientada positivamente, fronteira de uma região sólida W e F → um campo vetorial que tenha derivadas parciais contínuas em W , pelo Teorema de Gauss pode-se afirmar que:

∬ ∂ W   F → ⋅ n →   d s = ∭ w   d i v F →   d V

Em outras palavras, esse teorema afirma que, nessas condições acima, o fluxo de F → pela superfície ∂ W é igual à integral tripla do divergente desse campo em W . Quando você cair, então, nessa integral tripla, precisará usar aqueles recursos que você já aprendeu para resolvê-la: mudanças esféricas, cilíndricas etc, então é uma boa dar uma revisada nisso!

Tudo bem, agora que já vimos o Teorema de Gauss, vamos entender um pouco mais da utilidade dele! Da mesma forma que usamos o Teorema de Stokes como uma forma de calcular integrais de linha mais complicadas, quanto temos que calcular uma integral de superfície complicada, o Teorema de Gauss pode ser uma forma mais simples de calculá-la!

Exemplo: Calcule o fluxo ∬ S   F → . n →   d s , onde F → x , y , z = ( x y 2 ,   x 2 y ,   y ) e S é a superfície do sólido limitado pelo cilindro x 2 + y 2 = 1 e os planos z = 1 e z = - 1 , com a normal apontando para fora da superfície.

Passo 1: Vamos fazer um gráfico dessa região

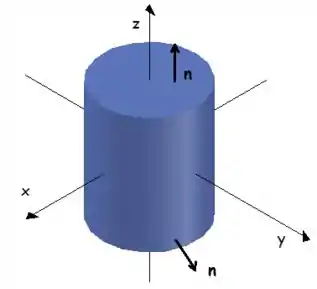
Como a região limitada por S é fechada e S está orientada positivamente, podemos aplicar o Teorema de Gauss, temos:

∬ S   F → . n → d s = ∭ w   d i v F →   d V

Passo 2: Calcular d i v F →

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z = y 2 + x 2

Passo 3: Montar a integral

∬ S   F → . n → d s = ∭ w   y 2 + x 2   d x d y d z

Onde W = { ( x , y , z ) | x 2 + y 2 ≤ 1 ;   - 1 ≤ z ≤ 1 } .

Passo 4: Vamos fazer, agora, a substituição cilíndrica.

x = r cos ⁡ θ

y = r   s e n   θ

z = z

J = r

A região passa a ser descrita como r ≤ 1 , 0 ≤ θ ≤ 2 π , - 1 ≤ z ≤ 1 e a integral passa a ser:

= ∫ - 1 1 ∫ 0 2 π ∫ 0 1 r cos ⁡ θ 2 + r   s e n   θ 2 r d r d θ d z =

= ∫ - 1 1 ∫ 0 2 π ∫ 0 1 r 3 d r d θ d z =

Passo 5: Resolver a integral

= ∫ - 1 1 ∫ 0 2 π r 4 4 r = 0 r = 1 d θ d z =

= 1 4 ∫ - 1 1 θ θ = 0 θ = 2 π d z =

= π 2 ∫ - 1 1 z z = - 1 z = 1 =

π

O Teorema de Gauss

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ - Cálculo 3 - P2 2010.1 – 1

Determine o fluxo do campo vetorial:

F = y 2 x + x x 2 + y 2 + z 2 , z 2 y + y x 2 + y 2 + z 2 , x 2 z + z x 2 + y 2 + z 2

Através da superfície do solido W limitado pelas esferas de equações: x 2 + y 2 + z 2 = a 2

x 2 + y 2 + z 2 = b 2

0 < a < b

Orientadas com sentidos opostos e exteriores ao sólido W .

Passo 1

Podemos ver que se trata de uma questão de Teorema de Gauss pois o campo em questão é muito complexo para se fazer a conta. Portanto, aplicando o Teorema:

∬ S   F ∙ d S → = ∭ W   d i v F d x d y d z

Calculando o divergente:

d i v F = x 2 + y 2 + z 2 + 1 x 2 + y 2 + z 2

Substituindo na fórmula, dá pra ver que o ideal é trabalhar com coordenadas esféricas:

∬ S   F ∙ d S → = ∭ W   x 2 + y 2 + z 2 + 1 x 2 + y 2 + z 2 d x d y d z

Passo 2

Mudando para coordenadas esféricas temos:

x = ρ   s e n ϕ cos ⁡ θ

y = ρ   s e n ϕ s e n θ

z = ρ cos ⁡ ϕ

θ ∈ 0,2 π

ϕ ∈ [ 0 , π ]

ρ ∈ a , b

E pelo Jacobiano temos o elemento de volume:

d x d y d z = ρ 2 s e n ϕ   d ρ d ϕ d θ

Passo 3

Substituindo:

∬ S   F ∙ d S → = ∫ 0 2 π ∫ 0 π ∫ a b ρ 2 + 1 ρ 2 ρ 2 s e n ϕ d ρ d ϕ d θ

Arrumando e calculando:

∬ S   F ∙ d S → = ∫ 0 2 π ∫ 0 π ∫ a b ρ 4 + 1 s e n ϕ d ρ d ϕ d θ

∬ S   F ∙ d S → = 2 π × - cos ⁡ ϕ 0 π × ρ 5 5 + ρ a b

∬ S   F ∙ d S → = 4 π b 5 - a 5 5 + b - a

Resposta

∬ S   F ∙ d S → = 4 π b 5 - a 5 5 + b - a

Exercício Resolvido #2

UFRJ - Cálculo 3 - P2 2014.1 – 2

Seja S a união das superfícies S 1 S 2 e S 3 dadas pelas equações abaixo:

S 1 : y = x 2 + z 2 ,     0 ≤ y ≤ 1 ;

S 2 : 1 = x 2 + z 2 ,     1 ≤ y ≤ 2 ;

S 3 : y = 3 - x 2 + z 2 ,     2 ≤ y ≤ 3 ;

Calcule ∬ S F → . n →   d S , onde F → é o campo de vetores definido por F → x , y , z = ( e cos ⁡ z ,   z 2 y + ln ⁡ x 2 + 1 ,   y 2 + x 2 z ) e n → é o campo de vetores normais unitários exterior à região limitada por S .

Passo 1

Vamos tentar imaginar como é o gráfico dessa superfície.

S 1 é um cone que tem o seu vértice na origem e vai aumentando o raio conforme o valor de y aumenta, até o ponto em que y = 1 , fazendo com que o raio do cone também valha 1 .

S 2 é um cilindro de raio 1 que começa no final do cone S 1 e vai até o ponto em que y = 2 .

S 3 é um paraboloide que “termina” em y = 3 e começa em y = 2 , partindo do final do cilindro S 2 .

Juntando tudo, temos o seguinte:

Como podemos ver, a superfície é toda fechada.

Para calcular ∬ S F → . n →   d S sobre uma superfície fechada, podemos usar o Teorema de Gauss.

Passo 2

O Teorema de Gauss é dado por:

∬ ∂ W   F → . n →   d s = ∭ w   d i v F →   d V

Onde:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

Passo 3

F → x , y , z = ( e cos ⁡ z ,   z 2 y + ln ⁡ x 2 + 1 ,   y 2 + x 2 z )

F 1 = e cos ⁡ z → ∂ F 1 ∂ x = 0

F 2 = z 2 y + ln ⁡ x 2 + 1 → ∂ F 2 ∂ y = z 2

F 3 = y 2 + x 2 z → ∂ F 3 ∂ z = x 2

O divergente será:

d i v F → = x 2 + z 2

Passo 4

∬ S   F → . n →   d s = ∭ w   x 2 + z 2 d V

Podemos escrever a região W como:

W = x 2 + z 2 ≤ 1 ,     x 2 + z 2 ≤ y ≤ 3 - x 2 + z 2

Pra simplificar o nosso cálculo, podemos usar coordenadas cilíndricas, onde:

x = r cos ⁡ θ

y = y

z = r sen ⁡ θ

J = r

Os limites para x e z são tranquilos, para descobrirmos os limites para y , basta substituir na relação que eu escrevi em W . Os limites são dados por:

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

r ≤ y ≤ 3 - r 2

Passo 5

Assim, a integral tripla será:

∭ w   x 2 + z 2 d V = ∫ 0 2 π ∫ 0 1 ∫ r 3 - r 2 r 2 r   d y d r d θ

= ∫ 0 2 π ∫ 0 1 ( 3 - r 2 - r ) r 2 r   d r d θ

= ∫ 0 2 π ∫ 0 1 3 r 3 - r 5 - r 4   d r d θ

= ∫ 0 2 π 3 r 4 4 - r 6 6 - r 5 5 0 1 d θ

= 2 π 3 4 - 1 5 - 1 6 = 23 π 30

Resposta

∬ S   F → . n →   d s = 23 π 30

Exercício Resolvido #3

UFRJ - Cálculo 3 - P2 2013.2 – 4

Considere o campo vetorial

F = z 2 , 2 y z , 4 cos ⁡ x .

Seja a ∈ ( 0,1 ) uma constante. Determine o fluxo de F através da superfície S definida como a fronteira da região

W = x , y , z : x 2 + y 2 + z 2 ≤ 1 ,     z ≤ a 1 - a 2 x 2 + y 2

Passo 1

Como o problema pede para calcularmos o fluxo de F através da superfície S , na verdade, ele está pedindo para calcularmos:

∬ S   F → . n → d S

E como se trata de uma superfície fechada, podemos usar o Teorema de Gauss, que diz que:

∬ S   F → . n →   d s = ∭ w   d i v F →   d V

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

Passo 2

F = z 2 , 2 y z , 4 cos ⁡ x

Vamos começar calculando as derivadas parciais dos componentes de F   → para o divergente.

F 1 = z 2 → ∂ F 1 ∂ x = 0

F 2 = 2 y z →   ∂ F 2 ∂ y = 2 z

F 3 = 4 cos ⁡ x → ∂ F 3 ∂ z = 0

Portanto,

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z = 2 z

Passo 3

A nossa região W é dada por:

W = x , y , z : x 2 + y 2 + z 2 ≤ 1 ,     z ≤ a 1 - a 2 x 2 + y 2

Isso significa que é a região no interior da esfera

x 2 + y 2 + z 2 = 1

E fora do cone

z ≤ a 1 - a 2 x 2 + y 2

O resultado é algo do tipo:

Passo 4

∬ S   F → . n →   d s = ∭ w   d i v F →   d V = ∭ W 2 z   d x d y d z

Como o nosso sólido é a parte de uma esfera, podemos usar coordenadas esféricas:

x = ρ sen ⁡ ϕ cos ⁡ θ

y = ρ sen ⁡ ϕ sen ⁡ θ

z = ρ cos ⁡ ϕ

J = ρ 2 s e n φ

Vamos usar o que o problema nos disse sobre a região W para descobrir os limites de ρ , ϕ e θ .

Passo 5

x 2 + y 2 + z 2 ≤ 1

Substituindo as coordenadas esféricas:

ρ 2 sen 2 ⁡ ϕ cos 2 ⁡ θ + ρ 2 sen 2 ⁡ ϕ sen 2 ⁡ θ + ρ 2 cos 2 ⁡ ϕ ≤ 1

cos 2 ⁡ θ + sen 2 ⁡ θ = 1

ρ 2 sen 2 ⁡ ϕ + ρ 2 cos 2 ⁡ ϕ ≤ 1

sen 2 ⁡ ϕ + cos 2 ⁡ ϕ = 1

ρ 2 ≤ 1

0 ≤ ρ ≤ 1

Passo 6

Ok, o que podemos fazer também é encontrar a interseção entre as superfícies:

x 2 + y 2 + z 2 = 1 → x 2 + y 2 = 1 - z 2

z = a 1 - a 2 x 2 + y 2 → x 2 + y 2 = z 2 1 - a 2 a 2

Igualando os dois termos:

1 - z 2 = z 2 1 - a 2 a 2

a 2 1 - z 2 = z 2 ( 1 - a 2 )

a 2 - a 2 z 2 = z 2 - a 2 z 2

z 2 = a 2

z = a

A interseção ocorre no plano z = a .

Como, de acordo com as coordenadas esféricas z = ρ cos ⁡ ϕ , a interseção ocorre quando

ρ = 1

z = cos ⁡ ϕ 0 = a

ϕ 0 = arccos ⁡ a

Então podemos ver inclusive no gráfico que

ϕ 0 ≤ ϕ ≤ π

Ah! Como não existem restrições para θ vamos utilizar os seus limites usuais:

0 ≤ θ ≤ 2 π

Passo 7

Ah! Existem outras maneiras de se encontrar esse ângulo ϕ 0 , então não precisa decorar do jeito que eu fiz.

Por exemplo, se você tenta usar só a equação:

z = a 1 - a 2 x 2 + y 2

Substituindo as coordenadas esféricas, você encontraria algo do tipo (já vou dar uma simplificada aqui, ok?):

cos ⁡ ϕ = a 1 - a 2 sen ⁡ ϕ

tan ⁡ ϕ = 1 - a 2 a

Nesse caso,

ϕ 0 = arctan ⁡ 1 - a 2 a

Po! Mas deu diferente, e agora?!

Cara, fica tranquilo, estamos falando do mesmo ângulo, então relaxa.

Uma outra forma seria igualar

z = 1 - x 2 - y 2

z = a 1 - a 2 x 2 + y 2

Substituindo as coordenadas esféricas, você encontraria algo do tipo (já vou dar uma simplificada aqui de novo, beleza?):

1 - ρ 2 sen 2 ⁡ ϕ = a 2 1 - a 2 ρ 2 sen 2 ⁡ ϕ

1 - ρ 2 sen 2 ⁡ ϕ - a 2 + a 2 ρ 2 sen 2 ⁡ ϕ = a 2 ρ 2 sen 2 ⁡ ϕ

ρ 2 sen 2 ⁡ ϕ = 1 - a 2

Considerando ρ = 1 (na superfície da esfera):

sen ⁡ ϕ = 1 - a 2

ϕ 0 = arcsen ⁡ 1 - a 2

Então

ϕ 0 = arccos ⁡ a = arcsen ⁡ 1 - a 2 = arctan ⁡ 1 - a 2 a

Dá no mesmo, estamos falando do mesmo ângulo.

Viu?! =]

Passo 8

Voltando pra integral:

∭ W 2 z   d x d y d z = ∫ 0 2 π ∫ ϕ 0 π ∫ 0 1 2 ρ cos ⁡ ϕ . ρ 2 sen ⁡ ϕ   d ρ   d ϕ   d θ

= 2 ∫ 0 2 π ∫ ϕ 0 π ∫ 0 1 ρ 3 cos ⁡ ϕ sen ⁡ ϕ   d ρ   d ϕ   d θ

= 2 ∫ 0 2 π ∫ ϕ 0 π ρ 4 4 cos ⁡ ϕ sen ⁡ ϕ 0 1   d ϕ   d θ

= 1 2 ∫ 0 2 π ∫ ϕ 0 π cos ⁡ ϕ sen ⁡ ϕ   d ϕ   d θ

Por substituição:

u = sen ⁡ ϕ

d u = cos ⁡ ϕ   d ϕ

Voltando pra integral:

= 1 2 ∫ 0 2 π ∫ u   d u   d θ

= 1 2 ∫ 0 2 π u 2 2   d θ

= 1 2   sen 2 ⁡ ϕ 2 ϕ 0 π ∫ 0 2 π d θ

= 1 2   sen 2 ⁡ ϕ 2 ϕ 0 π θ 0 2 π

= 1 4   ( sen 2 ⁡ π - sen 2 ⁡ ϕ 0 ) ( 2 π - 0 )

Onde:

sen ⁡ π = 0

sen ⁡ ϕ 0 = 1 - a 2

Portanto:

= π 2   0 - 1 - a 2

= - π 2   1 - a 2

Resposta

∬ S   F → . n →   d s = - π 2   1 - a 2

Exercício Resolvido #4

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 306-1.

Calcule ∬ S   F ∙ n d S , onde F = 2 x + x y 2 , - z y , z 2 2 - y 2 z , S é a superfície cilíndrica fechada limitada pelos planos z = 0 e z = 1 , cuja base no plano x y é limitada pelas curvas de equações:

x 2 + y - 1 2 = 4 ,     y ≥ 1

x 2 + y + 1 2 = 4 ,     y ≤ - 1

x - 2 2 + y 2 = 1 ,     x ≥ 2

x + 2 2 + y 2 = 1 ,     x ≤ - 2

E o vetor normal é exterior à S .

Passo 1

Pelo aspecto do campo vetorial, ficamos inclinados à aplicar o Teorema de Gauss:

∬ S   F ∙ n d S = ∭ W   d i v F d W

Calculando o divergente:

d i v F = 2 + y 2 - z + z - y 2

d i v F = 2

Passo 2

Agora precisamos determinar os limites de integração em W . Fazendo o desenho do cilindro, que não é tão difícil pois são vários semicírculos, obtemos:

Aplicando a fórmula, temos simplesmente o dobro do volume da região:

∬ S   F ∙ n d S = ∭ W   2 d W

∬ S   F ∙ n d S = 2 ∭ W   d W

∬ S   F ∙ n d S = 2 × V o l ( W )

Que é constituída basicamente de uma circunferência de raio 2 , uma de raio 1 e um retângulo de lados 4 e 2 . A altura é 1 .

V o l W = 1 × 2 2 π + 1 2 π + 4 × 2

V o l W = 5 π + 8

Substituindo:

∬ S   F ∙ n d S = 2 × 5 π + 8

Resposta

∬ S   F ∙ n d S = 10 π + 16

Exercício Resolvido #5

George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 545-24.

Dentre todos os sólidos retangulares definidos pelas desigualdades 0 ≤ x ≤ a , 0 ≤ y ≤ b , 0 ≤ z ≤ 1 , encontre aquela para o qual o fluxo exterior total de F = - x 2 - 4 x y i - 6 y z j + 12 z k através dos seis lados seja maior. Qual é o maior fluxo?

Passo 1

Para entender melhor nosso problema vamos somente rascunhar qual deve ser a imagem da superfície:

Então temos uma superfície retangular, a qual não sabemos parametizar, esse é um sinal de que seria bom usar o Teorema de Gauss!

Então vamos ver se é uma boa ideia!

Passo 2

O Teorema de Gauss nos diz que

∬ ∂ W   F → ⋅ n →   d s = ∭ w   d i v F →   d V

A integral, ∬ ∂ W   F → . n →   d s representa diretamente o fluxo sobre a superfície! E para calcular, o primeiro passso é saber qual o divergente do campo vetorial:

∇ ⋅ F =   ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

∇ ⋅ F = - 2 x - 4 y + - 6 z + 12 = 12 - 2 x - 4 y - 6 z

Passo 3

Agora vamos calcular a integral tripla com os intervalos:

0 ≤ x ≤ a , 0 ≤ y ≤ b , 0 ≤ z ≤ 1

∫ 0 a ∫ 0 b ∫ 0 1 12 - 2 x - 4 y - 6 z d z d y d x

∫ 0 a ∫ 0 b - 2 x - 4 y + 12 - 6 z 2 2 0 1 d y d x

∫ 0 a ∫ 0 b - 2 x - 4 y + 9 d y d x

∫ 0 a - 2 x y - 4 y 2 2 + 9 y 0 b d x

∫ 0 a - 2 x b - 2 b 2 + 9 b d x = - 2 b x 2 2 - 2 b 2 x + 9 b x 0 a =   - b a 2 - 2 b 2 a + 9 a b

Assim, o fluxo é dado por:

f a , b = a b ( - a - 2 b + 9 )

Passo 4

Para maximizar devemos ter

∂ f ∂ a = 0   e ∂ f ∂ b = 0

Assim,

∂ f ∂ a = - 2 a b - 2 b 2 + 9 b = 0

( - 2 a - 2 b + 9 ) b = 0

b = 0     o u   - 2 a - 2 b + 9 = 0

∂ f ∂ b =   - a 2 - 4 a b + 9 a = 0

- a - 4 b + 9 a = 0

a = 0   o u   - a - 4 b + 9 = 0  

Como o fluxo é

f a , b = a b ( - a - 2 b + 9 )

Se a = 0 ou   b = 0 , o fluxo também é zero.

Passo 5

Assim, devemos resolver o sistema:

( - 2 a - 2 b + 9 ) = 0 - a - 4 b + 9 = 0

Da segunda equação a = 9 - 4 b , substituindo na primeira:

2 9 - 4 b = 9 - 2 b

6 b = 9

b = 3 2

Logo,

a = 9 - 4 b = 3  

Resposta

O máximo fluxo é dado por:

f a , b = a b - a - 2 b + 9

f m a x = 27 2

Exercício Resolvido #6

UFRJ - Cálculo 3 - PF 2014.1 - 4

Calcule a integral

∬ ∂ Ω F → . n → d S

Onde F → x , y , z = x - y + z , y - z + x ,   z - x + y , ∂ Ω é a fronteira da região

Ω = ( x , y , z ) | x - y + z 2 + y - z + x 2 + z - x + y 2 ≤ 1

Orientada com a normal n → exterior.

Passo 1

Como ∂ Ω é a fronteira de uma região (um volume), sabemos que essa superfície é fechada. Como o campo e a parametrização aqui são muito complicados, vamos tentar usar Gauss, ok?

Vamos começar calculando o divergente disso aí:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

d i v F → = 1 + 1 + 1 = 3

Passo 2

Show, agora vamos aplicar o teorema:

∬ ∂ Ω   F → . n → d S = ∭ Ω   d i v F →   d V = 3 ∭ Ω   d V

Passo 3

Agora precisamos de uma mudança de variáveis. Repara que se a gente fizer a mudança:

x - y + z = u

y - z + x = v

z - x + y = w

A gente consegue fazer essa superfície virar uma esfera, viu?

Isso nos dá

u 2 + v 2 + w 2 ≤ 1

Bom, precisamos do Jacobiano disso aí, temos:

x = u + v 2

y = v + w 2

z = u + w 2

O que nos dá:

∂ x ∂ u = 1 2

∂ x ∂ v = 1 2

∂ x ∂ w = 0

∂ y ∂ u = 0  

∂ y ∂ v = 1 2

∂ y ∂ w = 1 2

∂ z ∂ u = 1 2

∂ z ∂ v = 0

∂ z ∂ w = 1 2

Agora tem que saber calcular determinante, galera, não tem jeito. Vamos usar aquele método que selecionamos os termos da primeira linha e vamos calculando determinantes 2 × 2 e multiplicando pelos seus valores:

J = 1 / 2 1 / 2 0 0 1 / 2 1 / 2 1 / 2 0 1 / 2 = 1 2 × 1 4 + 1 2 × 1 4 + 0 = 1 8 + 1 8 = 1 4

Ufa.

Passo 4

Agora fazemos a mudança:

∬ ∂ Ω   F → . n → d S = 3 ∭ e s f e r a   1 4 d V = 3 4 V o l u m e e s f e r a

Como o volume da esfera de raio 1 é 4 3 π :

∬ ∂ Ω   F → . n → d S = π

Resposta

π

Exercícios de Livros Relacionados

Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,