Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Alterações na Mudança de Variável

Ver Todos os Exercícios

Teoria

Deslocamentos nas mudanças

Galera, imaginem que a nossa região de integração é essa esfera aqui embaixo:

x - 1 2 + y 2 + z 2 = 1

Primeiro, vamos tentar a substituição esférica normal:

x = ρ   s e n   φ   c o s   ,     y = ρ   s e n   φ   s e n   θ ,     z = ρ cos ⁡ φ

Levando isso para a esfera:

ρ   s e n   φ   c o s   θ - 1 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 = 1

ρ 2 s e n 2 φ cos 2 ⁡ θ - 2 ρ   s e n   φ   c o s   θ + 1 + ( ρ 2 s e n 2 φ )   s e n 2 θ + ρ 2 cos 2 ⁡ φ = 1

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ - 2 ρ   s e n   φ   c o s   θ + 1 = 1

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ = 2 ρ   s e n   φ   c o s   θ

ρ 2 = 2 ρ   s e n   φ   c o s   θ → ρ = 2   s e n   φ   c o s   θ

Meio chata essa expressão, não é? Agora vamos tentar fazer essa substituição aqui:

x = ρ   s e n   φ   c o s   θ + 1 ,     y = ρ   s e n   φ   s e n   θ ,     z = ρ cos ⁡ φ

Olha o que acontece:

ρ   s e n   φ   c o s   θ + 1 - 1 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 = 1

ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 = 1

ρ 2 s e n 2 φ cos 2 ⁡ θ + ( ρ 2 s e n 2 φ )   s e n 2 θ + ρ 2 cos 2 ⁡ φ = 1

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ = 1 → ρ = 1

Viu que a esfera voltou a ser uma expressão bonitinha? O que a gente fez foi mudar o centro das coordenadas esféricas para o centro da esfera ( 1,0 , 0 ) . Assim, a distância dos pontos da esfera à (nova) origem passa a ser constante e a expressão dela passa a ser ρ = r a i o .

Mas como a gente fez isso? Somando as coordenadas do centro da esfera nas variáveis da mudança esférica. Basicamente, você tem que somar números a x ,   y e z que cancelem as constantes “soltas” nos termos quadráticos da equação. Resumindo, é o seguinte:

Para uma esfera do tipo

x - a 2 + y - b 2 + z - c 2 = r a i o 2

Geralmente, faremos a mudança

x = ρ   s e n   φ   c o s   θ + a

y = ρ   s e n   φ   s e n   θ + b

z = ρ cos ⁡ φ + c

A esfera vai passar a ser escrita como ρ = r a i o . Pode fazer essa mudança para conferir.

Beleza, mas e o jacobiano? O que acontece com ele?

Lembra que o jacobiano é calculado por derivadas parciais dos termos da mudança? Bom, a derivada de uma constante não é zero? Então todos esses termos a ,   b e c vão desaparecer! Portanto: sempre que somamos ou substraímos constantes em uma mudança de variáveis o seu jacobiano não se altera. Logo:

J = ρ 2 s e n φ

Bom, já que falamos de coordenadas esféricas, vamos falar das coordenadas cilíndricas também. Seguindo o mesmo raciocínio, quando encontramos um cilindro deslocado da origem do tipo:

x - a 2 + y - b 2 = r a i o 2

Nós podemos fazer a mudança cilíndrica:

x = r cos ⁡ θ + a

y = r   s e n   θ + b

z = z

J = r

Isso nos dá:

r cos ⁡ θ + a - a 2 + r   s e n   θ + b - b 2 = r a i o 2 → r = r a i o

O jacobiano não se altera, novamente! Dessa forma, a distância dos pontos do cilindro ao eixo z passa a ser constante e ele passa a ser descrito como r = r a i o .

Recapitulando: quando você encontrar regiões que pareçam perfeitas para a mudança esférica ou cillíndrica, porém não estejam centradas na origem, às vezes vale à pena fazer essas mudanças com centro deslocado. Mas muito cuidado: não é só porque você tem uma superfície deslocada que vai valer à pena fazer isso! Em geral, usamos esse artifício quando a região toda é centrada em algum eixo/ ponto.

Então, depois de fazer a mudança e encontrar os intervalos das variáveis, a questão vira qualquer outra questão de integrais triplas, não tem mistério!

Mudança de eixos

Aqui a gente vai ter uma situação desse tipo

Bom, já que é um cilindro, vamos usar coodenadas cilíndricas, certo:

x = r cos ⁡ θ ,     y = r   s e n   θ ,     z = z ,     J = r

Levando isso para e equação do cilindro:

y 2 + z 2 = 1

r   s e n   θ 2 + z 2 = 1

Agora, nas equações dos planos:

x = 1 = r cos ⁡ θ

x = 2 = r cos ⁡ θ

Nossa, ficou tudo horrível, né? Mas porque?

Isso aconteceu porque as coordenadas cilíndricas são definidas com simetria em relação ao eixo z , olha só:

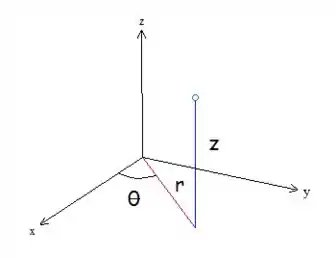
Então, as superfícies que tem simetria nesse eixo tendem a ficar mais simples escritas nessas coordenadas. Mas, nosso cilindro do exemplo está “deitado” com simetria no eixo x , por isso não conseguimos agrupar termos na mudança e a expressão dele ficou zoada.

Ah, então não tem o que fazer? Não usamos essa mudança? Claro que não, nós só vamos usar uma mudança cilíndrica diferente.

Vamos criar uma mudança cilíndrica que tenha simetria em x ! Quando a simetria era em z , repare que a única coordenada que não se altera é essa:

x = r cos ⁡ θ ,     y = r   s e n   θ ,     z = z

Então, a coordenada que não vai se alterar agora é a x : É como se o eixo x “virasse” o eixo z . Então vamos ter

y = r cos ⁡ θ ,     z = r   s e n   θ ,     x = x

Pronto, essa é nossa mudança! Isso é um macete para você não se perder. O jacobiano não muda:

J = r

Vamos tentar fazer essa nova mudança nas nossas superfícies então:

y 2 + z 2 = 1

r   c o s   θ 2 + r   s e n   θ 2 = 1

r 2 = 1 → r = 1

Agora, nas equações dos planos:

x = 1

x = 2

A região é definida então por 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π e 1 ≤ x ≤ 2 .

Muito mais simples, não?

Lembrando que, como definimos as coordenadas cilíndricas com simetria em x , o raio r é marcado a partir desse eixo e o ângulo θ é marcado ao redor dele (no plano y z ). É como se o x fosse o novo z !

Mudança com denominadores diferentes

Digamos que você precise calcular uma integral tripla no interior da região:

4 x 2 + y 2 = 1

Isso é um cilindro de seção elíptica:

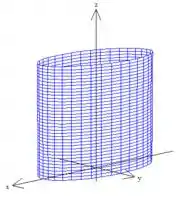
Bom, já que é um cilindro, vamos tentar coordenadas cilíndricas, não é?

x = r cos ⁡ θ ,     y = r   s e n   θ ,       z = z

Se você substituir na equação do cilindro vai ver que vai ficar horrível! Porque o cilindro não ficará r = r a i o bonitinho como estamos acostumados a ver. Porque isso? Porque ele não tem seção circular! Então, na mudança de variáveis os termos não vão se agrupar certinho, por causa daquele coeficiente 4 em x 2 .

E se a gente desse um jeito de sumir com esse coeficiente? Olha o que acontece quando fazemos essa substituição aqui:

x = 1 2 r cos ⁡ θ ,     y = r   s e n θ ,     z = z

Levando para o cilindro:

4 1 2 r cos ⁡ θ 2 + ( r   s e n   θ ) 2 = 1

r 2 cos 2 ⁡ θ + r 2 s e n 2 θ = 1

r 2 = 1 → r = 1

Viu que o 1 / 2 que adicionamos à mudança cancelou aquele coeficiente 4 ? Aí a expressão do cilindro ficou beem melhor. É como se a gente tivesse “transformado” sua seção em circular.

Mas e o que acontece com o Jacobiano da mudança? Esse coeficiente vai para ele:

J = 1 2 r

Esse tipo de mudança pode ser muito útil quando temos cilindros de seção elíptica, pois ele faz o raio passar a ser constante e simplifica muito as coisas! Claro que temos que fazer a mesma mudança em todas as superfícies que estiverem limitando a região. A partir daí, a questão vira uma questão qualquer de integral tripla.

Então, quando temos um cilindro do tipo:

x 2 a 2 + y 2 b 2 = 1

Podemos pensar na mudança:

x = a   r cos ⁡ θ

y = b   r   s e n   θ

z = z

J = a b   r

Vamos ver um outro caso agora. Quando temos um elipsoide do tipo:

x 2 a 2 + y 2 b 2 + z 2 c 2 = 1

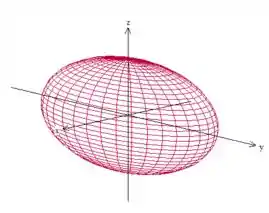
Isso se parece muito com uma esfera, não é? Porém se tentarmos a substituição esférica, vamos encontrar uma expressão meio zoada que nem aconteceu com o cilindro. Isso porque, novamente, o raio da superfície não é constante.

Mas se a gente fizer uma substituição do tipo:

x = a   ρ   s e n   φ   c o s   θ

y = b   ρ   s e n   φ   s e n   θ

z = c   ρ cos ⁡ φ

J = a b c   ρ 2 s e n φ

Os coeficientes do elipsoide vão “sumir” e vamos encontrar um ρ constante.

Isso porque esses coeficientes que acrescentamos à mudança esférica vão cancelar os coeficientes do elipsoide, “transformando” ele na esfera ρ = 1 . Lembrando que os coeficientes vão todos para o Jacobiano.

Show? Então, quando você encontrar um elipsoide pode pensar em fazer esse tipo de mudança esférica. O resto da questão fica o mesmo passo a passo de sempre!

Beleza? Vamos treinar isso aí!

Mudança de eixos

Mudança com denominadores diferentes

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ - Cálculo 3 - P1 2013.1 – 4

Calcule o valor da integral

∭ D   ( x 2 + y 2 + z 2 )   d x d y d z

Onde D = { ( x , y , z ) ∈ R 3 | x 2 + y 2 + z 2 ≤ x } .

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Completando o quadrado da expressão da superfície, temos:

x 2 - x + y 2 + z 2 = 0

x - 1 2 2 + y 2 + z 2 = 1 4

Uma esfera de raio 1 / 2 centrada em ( 1 / 2 ,   0 ,   0 ) , portanto, deslocada no eixo x .

Passo 2

Essa região de integração parece simples, não é? Sim, mas, quando fazemos a mudança para coordenadas esféricas , como temos feito até agora, a integral se torna uma expressão não muito agradável, envolvendo sen 6   e cos 5 ⁡   . Vamos, então, tentar contornar esse problema.

Uma esfera centrada na origem é escrita em coordenadas polares como ρ = ( raio ) , como já vimos. Essa esfera do problema, por estar deslocada, seria escrita como ρ = sen ⁡ φ cos ⁡ θ . Mas porque temos agora essa expressão bem mais complicada? Porque agora, não temos mais a simetria em relação à origem, pois a distância dos pontos da esfera ao ponto ( 0,0 , 0 ) não é mais constante.

Temos, então, duas saídas para tornar a região de integração mais simétrica em relação aos eixos coordenados.

Solução 1: Essa solução é a mais abrangente. Se você reparar, as coordenadas esféricas são definidas com uma certa simetria em relação ao eixo z . Como assim? O ângulo θ é medido em torno desse eixo e o ângulo φ , a partir desse eixo. Por isso, quando temos uma esfera deslocada em z , sua equação não fica tão complicada como quando está deslocada nos outros eixos.

Partindo dessa ideia, podemos, então, fazer uma mudança esférica diferente, atribuindo ( ρ cos ⁡ φ ) não ao eixo z , mas ao eixo de simetria da região, no caso, o eixo x . Teremos, então:

y = ρ sen ⁡ φ cos ⁡ θ

z = ρ sen ⁡ φ sen ⁡ θ

x = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

Dessa forma a esfera seria escrita como ρ = cos ⁡ φ . Essa solução seria muito útil se tivéssemos uma região mais complexa com simetria em x .

Solução 2: Provavelmente essa forma é a mais intuitiva, mais fácil de visualizar. A esfera não está centrada na origem? Leve a origem a ela então! Como assim? A esfera está deslocada em x , não é? Em vez de definirmos x = ρ   s e n   φ   c o s   θ , vamos definir   x - 1 / 2 = ρ   s e n   φ   c o s   θ , o que nos dá:

x = ρ   sen ⁡ φ cos ⁡ θ + 1 / 2

y = ρ   sen ⁡ φ sen ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

É como se você tivesse levado a origem para o ponto ( 1 / 2 ,   0,0 ) . Veja que, substituindo esses valores na equação da esfera, temos:

x - 1 2 2 + y 2 + z 2 = 1 4   →   ρ   sen ⁡ φ cos ⁡ θ 2 + ρ   sen ⁡ φ sen ⁡ θ 2 + ρ cos ⁡ φ 2 = 1 4

ρ = 1 / 2

Temos, agora, uma expressão muito mais simples para a esfera. Talvez você esteja se perguntando: o Jacobiano não muda? Não, porque quando adicionamos ou subtraímos uma constante na mudança de variáveis, a derivada desse termo é zero, logo, o Jacobiano não se altera!

Aqui, vamos optar por essa solução.

Passo 3

Utilizando essa substituição, a região de integração é escrita como:

D = { ( ρ , θ , φ ) | 0 ≤ θ ≤ 2 π ; 0 ≤ φ ≤ π ;   0 ≤ ρ ≤ 1 / 2 }

Exatamente como uma esfera centrada na origem.

Passo 4

Vamos agora escrever o termo x 2 + y 2 + z 2 em função das novas variáveis.

x 2 + y 2 + z 2 = ρ sen ⁡ φ cos ⁡ θ + 1 2 2 + ρ sen ⁡ φ sen ⁡ θ 2 + ρ cos ⁡ φ 2 =

ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ   + ρ sen ⁡ φ cos ⁡ θ + 1 4 + ρ 2 sen 2 ⁡ φ sen 2 ⁡ θ + ρ 2 cos 2 ⁡ φ =

= ρ 2 sen 2 ⁡ φ + ρ sen ⁡ φ cos ⁡ θ + 1 4 + ρ 2 cos 2 ⁡ φ   =

= ρ 2 + ρ sen ⁡ φ cos ⁡ θ + 1 4  

Montando agora a integral iterada, temos:

∫ 0 π ∫ 0 2 π ∫ 0 1 2   ρ 2 + ρ sen ⁡ φ cos ⁡ θ + 1 4   ρ 2 sen ⁡ φ d ρ   d θ   d φ =

∫ 0 π ∫ 0 2 π ∫ 0 1 2 ρ 4 sen ⁡ φ + ρ 3 sen 2 ⁡ φ cos ⁡ θ + ρ 2 sen ⁡ φ 4 d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π ∫ 0 2 π ρ 5 sen ⁡ φ 5 + ρ 4 4 sen 2 ⁡ φ cos ⁡ θ + ρ 3 sen ⁡ φ 12 ρ = 0 ρ = 1 / 2   d θ   d φ =

= ∫ 0 π ∫ 0 2 π sen ⁡ φ 5 × 32 + sen 2 ⁡ φ cos ⁡ θ 16 × 4   + sen ⁡ φ 12 × 8 d θ   d φ =

= ∫ 0 π ∫ 0 2 π sen ⁡ φ 60 + sen 2 ⁡ φ cos ⁡ θ 64 d θ   d φ =

Passo 6

Agora vamos integrar em relação a θ :

= ∫ 0 π θ sen ⁡ φ 60 + sen 2 ⁡ φ sen ⁡ θ 64   θ = 0 θ = 2 π     d φ =

= ∫ 0 π π sen ⁡ φ 30     d φ =

Passo 7

Finalmente, integrando em relação a φ :

= π cos ⁡ φ 30 0 π =

= π ( 1 - ( - 1 ) ) 30 =

Resposta

π 15

Exercício Resolvido #2

USP - Cálculo 3 - PSUB 2015 – 1

Calcule a massa da região x 2 + y 2 + z - 1 2 ≤ 2 com função densidade δ x , y , z = 2 + z .

Passo 1

O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por δ x , y , z . Nós sabemos que:

d m =   δ x , y , z d V

Onde d m é o diferencial de massa e d V o de volume. Integrando ambos os lados na região W em que o sólido está contido, temos que:

M = ∭ W   δ x , y , z d V

M = ∭ W   2 + z   d x d y d z

Passo 2

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio 2 centrada em ( 0,0 , 1 ) :

A região do problema é o que está dentro da esfera, beleza?

Passo 3

Como a região é limitada por uma esfera, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Na verdade, para facilitar um pouco a vida, vamos usar coordenadas esféricas deslocadas, ok?

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ + 1

J = ρ 2 s e n   φ

Assim, o centro das coordenadas é o centro da esfera, isso vai nos ajudar bastante.

Passo 4

Precisamos escrever matematicamente a região de integração. Como nós deslocamos as coordenadas para o centro da esfera, ela passa a ser escrita como ρ = r a i o , no caso:

ρ = 2

Você pode verificar isso fazendo a mudança esférica na sua equação!

x 2 + y 2 + z - 1 2 ≤ 2

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ + 1

O termo - 1 da equação vai ser cancelado pelo + 1 da mudança esférica.

Bom, como se trata da esfera inteira, 0 ≤ θ ≤ 2 π ; 0 ≤ φ ≤ π , o que nos dá:

W = ρ , θ , φ 0 ≤ θ ≤ 2 π ; 0 ≤ φ ≤ π ;   0 ≤ ρ ≤ 2

Passo 5

Vamos agora fazer a substituição esférica na integral:

M = ∭ W   2 + z   d x d y d z

= ∫ 0 π ∫ 0 2 π ∫ 0 2 2 + ρ cos ⁡ φ + 1 ρ 2 s e n   φ   d ρ d θ d φ =

= ∫ 0 π ∫ 0 2 π ∫ 0 2 ρ 3 s e n   φ cos ⁡ φ + 3 ρ 2 s e n   φ d ρ d θ d φ =

Passo 6

Agora vamos integrar em relação a ρ :

= ∫ 0 π / ∫ 0 2 π ρ 4 4 s e n   φ cos ⁡ φ + ρ 3 s e n   φ 0 2 d θ d φ =

= ∫ 0 π / ∫ 0 2 π s e n   φ cos ⁡ φ + 2 2 s e n   φ d θ d φ =

Passo 7

Agora em relação a θ :

= 2 π ∫ 0 π s e n   φ cos ⁡ φ + 2 2 s e n   φ   d φ =

Passo 8

Agora vamos integrar em relação a φ :

= 2 π 1 2 s e n 2   φ - 2 2 cos ⁡ φ   0 π =

= 2 π 0 + 2 2 - 0 - 2 2 =

= 8 π 2

Resposta

8 π 2

Exercício Resolvido #3

USP - Cálculo 3 - P1 2014 – 2

Calcule a integral

∭ E   x z   d x d y d z

Sobre a região E = { x , y , z : x 2 + y 2 + z 2 ≤ 36   e   z ≥ x 2 + y - 6 2 ,   x ≥ 0 } .

Passo 1

Vamos fazer um esboço da região W para entender melhor o que está sendo pedido. Temos uma esfera de raio 6 centrada na origem e um cone, dado pela equação z ≥ x 2 + y - 6 2 . Repare que, no lugar de onde costumamos ter “ y ”, temos ( y - 6 ) , isso quer dizer que o cone não está centrado em y = 0 , mas sim em y = 6 , na verdade, no ponto ( 0,6 , 0 ) .

Vamos desenhar isso aí então:

Repare que o problema também diz que x ≥ 0 . Temos algo assim então:

Nossa região é a que está dentro da esfera e acima do cone. Beleza?

Como podemos ver, em z o sólido é limitado embaixo pelo cone z = x 2 + y - 6 2 e em cima pela esfera x 2 + y 2 + z 2 = 36 .   No plano x y , temos um domínio D , com o qual não vamos nos preocupar por enquanto. Vamos, então, escrever essa região como tipo I:

E = { ( x , y , z ) | x , y ∈ D ;   x 2 + y - 6 2 ≤ z ≤ 36 - x 2 - y 2 }

Passo 2

Vamos agora substituir os intervalos que encontramos na integral iterada:

∬ D   ∫ x 2 + y - 6 2 36 - x 2 - y 2 x z   d z d x d y

Passo 3

Integrando em relação a z , temos:

= ∬ D   x z 2 2 x 2 + y - 6 2 36 - x 2 - y 2 d x d y =

= 1 2 ∬ D   36 - x 2 - y 2 - x 2 - y - 6 2 x d x d y =

= 1 2 ∬ D   - 2 x 2 - 2 y 2 + 12 y x d x d y =

= - ∬ D   x 2 + y 2 - 6 y x d x d y =

Passo 4

Agora vamos descrever essa região D , que é a projeção do sólido no plano x y . Antes de tudo, temos que fazer a interseção entre essas duas curvas, certo? Descobrir qual é a curva que elas formam no plano x y . Para isso, precisamos igualar a equação da esfera à do cone:

z = x 2 + y - 6 2 = 36 - x 2 - y 2

2 x 2 + y 2 - 12 y + 36 = 36 - x 2 - y 2

x 2 + y 2 - 6 y = 0

Agora nós completamos o quadrado do termo y , desse jeito:

x 2 + y - 3 2 ⏟ y 2 - 6 y + 9 = 9

Quando nós substituímos y 2 - 6 y por y - 3 2 , acabamos adicionando à equação um temos 9 que não existia, por isso, tivemos que compensar com um 9 do outro lado.

Não podemos nos esquecer de que x ≥ 0 !

Bom, isso aí é parte de uma circunferência de raio 3   deslocada da origem, não é? Ela está centrada em ( 0,3 ) :

Essa imagem representa o sólido E visto de cima, esse é o nosso domínio D . Como se trata de uma circunferência, vamos usar coordenadas polares, né? Já que a circunferência está deslocada para ( 0,3 ) , vamos fazer a seguinte substituição polar:

x = r cos ⁡ θ

y = r sen ⁡ θ + 3

J = r

Por que isso? Porque, quando aplicarmos isso à equação x 2 + y - 3 2 = 9 esse + 3 vai sumir e ela vai se transformar em apenas r = 3 . É como se estivéssemos trazendo o centro dos novos eixos coordenados para o centro na circunferência. Podemos dizer, então, que - π / 2 ≤ θ ≤ π / 2 (imagine o centro dos eixos coordenados no centro da circunferência).

Não gostou disso? Faz a substituição polar normal então, você só vai encontrar algumas expressões mais trabalhosas, os intervalos de integração serão diferentes, mas está certo do mesmo jeito!

Temos, então, 0 ≤ r ≤ 3 e - π / 2   ≤ θ ≤ π / 2

Substituindo na integral:

= - ∬ D   x 2 + y 2 - 6 y x d x d y =

= - ∫ - π / 2 π / 2 ∫ 0 3 r 2 cos 2 ⁡ θ + r   s e n   θ + 3 2 - 6 r   s e n   θ + 3 r 2 cos ⁡ θ d r d θ =

= - ∫ - π / 2 π / 2 ∫ 0 3 r 2 + 9 - 18 r 2 cos ⁡ θ d r d θ =

= - ∫ - π / 2 π / 2 ∫ 0 3 r 2 - 9 r 2 cos ⁡ θ d r d θ =

= - ∫ - π / 2 π / 2 ∫ 0 3 r 4 - 9 r 2 cos ⁡ θ d r d θ =

Passo 5

Agora vamos começar integrando em relação a r :

= - ∫ - π / 2 π / 2 r 5 5 - 3 r 3 cos ⁡ θ 0 3 d θ =

= - 162 5 ∫ - π / 2 π / 2 cos ⁡ θ d θ =

Passo 6

Agora em relação a θ :

= 162 5 s e n   θ - π / 2 π / 2 =

= 162 5 1 - - 1 =

= 162 5 2

= 324 5

Resposta

324 5

Exercício Resolvido #4

Elaboração Própria

Seja W o sólido limitado por x = 4 y 2 + 4 z 2 e pelo plano x = 4 . Calcule

∭ W x d V

Passo 1

Antes de tudo, vamos fazer um esboço da nossa região, para entendermos melhor o que está sendo pedido. Vemos que x = 4 y 2 + 4 z 2 é a equação de um paraboloide, mas com simetria em x. O outro cara é um plano x = 4 . Portanto, temos a seguinte região

Passo 2

Como a região é limitada por um paraboloide e um plano e a função a ser integrada f x , y , z = x não pede nenhuma mudança específica, vamos usar a mudança cilíndrica.

x = x

y = r cos ⁡ θ

z = r sen ⁡ θ

J = r

Passo 3

Precisamos escrever, matematicamente, a nossa região.

Lembre-se que as variáveis r , θ normalmente vão ser descobertas da interseção entre os caras envolvidos, ou seja, precisamos achar a interseção do plano com o paraboloide. Como fazemos isso? Igualando as expressões.

x = 4 , x = 4 y 2 + 4 z 2 → 4 y 2 + 4 z 2 = 4 → y 2 + z 2 = 1

Portanto, r ,   θ vão variar dentro desse círculo, ou seja, 0 ≤ r ≤ 1 e 0 ≤ θ ≤ 2 π .

Precisamos agora determinar a variação de x . Veja na figura que ele varia da equação do paraboloide até a equação do plano, ou seja

x = 4 y 2 + 4 z 2 → x = 4 r 2

x = 4 → x = 4

Portanto, nossa região descrita matematicamente será

W = { ( r , θ , x ) | 0 ≤ r ≤ 1 ,   0 ≤ θ ≤ 2 π ,   4 r 2 ≤ x ≤ 4 }

Passo 4

Vamos agora (finalmente) fazer a substituição esférica na integral:

∭ W x d V

= ∫ 0 2 π ∫ 0 1 ∫ 4 r 2 4 x r d x d r d θ =

Passo 5

Vamos realizar a integração em x

= 1 2 ∫ 0 2 π ∫ 0 1 r x 2 4 r 2 4 d r d θ =

= 1 2 ∫ 0 2 π ∫ 0 1 r 16 - 16 r 4 d r d θ =

= 8 ∫ 0 2 π ∫ 0 1 r 1 - r 4 d r d θ =

Passo 6

Realizando a integração em r

= 8 ∫ 0 2 π r 2 2 - r 6 6   0 1 d θ =

= 8 ∫ 0 2 π 1 2 - 1 6 d θ =

16 π 3

Resposta

16 π 3

Exercício Resolvido #5

UFRJ, Cálculo III, P1/2013.2, 3

Seja W ⊂ R 3 o sólido que resulta da interseção das regiões 9 x 2 + 4 y 2 ≤ 36 , 3 3 2 x ≤ y , x ≥ 0 , z ≥ 0 e z ≤ y + 1 , calcular o volume de W .

Passo 1

Vamos fazer um esboço da região W para entender melhor o que está sendo pedido:

Essa região é um pouco confusa mesmo, vamos por partes.

Temos um cilindro de base elíptica dado por 9 x 2 + 4 y 2 = 36 (em azul).

O plano vertical x = 0 está representado em cinza.

A equação 3 3 2 x = y representa no plano x y uma reta, certo? No R 3 ela independe de z , então temos essa reta ao longo de z , gerando um plano vertical. Como o coeficiente angular 3 3 2 é positivo, essa reta corta o 1 º e o 3 º quadrante. A parte que vai nos interessar é onde x , y > 0 , como na figura.

O plano z = 0 limita a região por baixo, é fácil visualizar. Falta, agora, o plano z = y + 1 , representado em verde. Podemos interpretá-lo como a reta z = y + 1 do plano y z repetida ao longo de eixo x .

Essa é a região vista de cima, para você entender melhor:

Passo 2

Agora precisamos escrever matematicamente essa região W . Como o sólido possui simetria em relação ao eixo z e é limitado lateralmente por um cilindro, vamos usar coordenadas cilíndricas. Faremos:

x = 2 r cos ⁡ θ

y = 3 r sen ⁡ θ

z = z

J = 6 r

Perceba que o cilindro possui base elíptica! Por isso adicionamos esses coeficientes 2 e 3 na substituição.

Passo 3

Vamos, agora, descobrir os intervalos de integração. Vamos começar pela variação de r .

9 x 2 + 4 y 2 = 36 → 9 ( 2 r cos ⁡ θ ) ^ 2 + 4 ( 3 r sen ⁡ θ ) 2 = 36 →  

36 r 2 ( cos 2 ⁡ θ + sen 2 ⁡ θ ) = 36 ∴ r = 1

Assim, temos que a variação de r será 0 ≤ r ≤ 1 .

Passo 4

Pelo gráfico, vemos que os valores de θ variam desde o plano 3 3 2 x = y até o plano x = 0 , o que nos dá θ i ≤ θ ≤ π / 2 , certo? Vamos, então, fazer a substituição cilíndrica na equação desse plano pra descobrir o outro valor desse θ i :

3 3 2 2 r cos ⁡ θ i = 3 r   sen ⁡ θ i

3 cos ⁡ θ i = sen ⁡ θ i   → tg ⁡ θ i = 3   →   θ i = π / 3

Temos, então, π / 3 ≤ θ ≤ π / 2 .

Passo 5

Agora só falta o intervalo de z . Veja que o sólido está limitado embaixo pelo plano z = 0 e em cima pelo plano inclinado z = y + 1 (por isso é muito importante que você entenda a região de integração). Vamos, então, fazer a mudança de variáveis nesse plano:

z = 3 r   sen ⁡ θ + 1

Temos, então 0 ≤ z ≤ 3 r sen ⁡ θ + 1 . Assim, nossa região de integração será escrita como:

W = { ( r , θ , z ) | π / 3 ≤ θ ≤ π / 2 ; 0 ≤ r ≤ 1 ;   0 ≤ z ≤ 3 r   sen ⁡ θ + 1   }

Passo 6

Vamos agora substituir os intervalos que encontramos na integral iterada:

∫ π / 3 π / 2 ∫ 0 1 ∫ 0 3 r   sen ⁡ θ + 1   6 r d z d r d θ =

Passo 7

Integrando em relação a z , temos:

= ∫ π / 3 π / 2 ∫ 0 1 6 r z z = 0 z = 3 r   sen ⁡ θ + 1 d r d θ =

= ∫ π / 3 π / 2 ∫ 0 1 6 r ( 3 r   sen ⁡ θ + 1 ) d r d θ =

= ∫ π / 3 π / 2 ∫ 0 1 18 r 2   sen ⁡ θ + 6 r   d r d θ =

Passo 8

Agora, integramos em relação a r :

= ∫ π / 3 π / 2 18 r 3 3 sen ⁡ θ + 6 r 2 2 r = 0 r = 1 d θ =

= ∫ π / 3 π / 2 6 sen ⁡ θ + 3 d θ =

Passo 9

Finamente, integramos em relação a θ :

= - 6 cos ⁡ θ + 3 θ π / 3 π / 2 =

= 0 + 3 π 2 - - 6 . 1 2 + 3 π 3 =

Resposta

π 2 + 3

Exercício Resolvido #6

George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson, 2009, pp. 459-20.

Encontre o volume do elipsoide

x 2 a 2 + y 2 b 2 + z 2 c 2 = 1

(Sugestão: Sejam x = a u ,   y = b v ,   z = c w . Então encontre o volume sobre uma região apropriada no espaço u v w . )

Passo 1

Esse elipsoide tem a seguinte imagem,

Veja que ele parece um pouco com uma esfera! Como queremos o volume do elipsoide, vamos resolver a integral

V = ∭ W   d x d y d z

A sugestão do exercício é de fazer a seguinte mudança de variáveis, x = a u ,   y = b v ,   z = c w , assim, o volume seria

V = ∭ W   d x d y d z = ∭ T J u , v , w d u d v d w

Para isso, precisamos calcular o jacobiano!

Passo 2

O jacobiano é calculado por,

J ( u ,   v , w ) = ∂ x , y , z ∂ ( u , v , w ) = d x d u d x d v d x d w d y d u d y d v d y d w d z d u d z d v d z d w

Como, x = a u ,   y = b v ,   z = c w

d x d u = a , d x d v = d x d w = 0

d y d u = 0 , d y d v = b , d y d w = 0

d z d u = 0 , d z d v = 0 , d z d w = c

Desta forma temos o determinante,

J u ,   v , w = a 0 0 0 b 0 0 0 c = a b c

Passo 3

Ao fazer esta mudança de variáveis nosso elipsoide fica com a forma,

a 2 u 2 a 2 + b 2 v 2 b 2 + c 2 w 2 c 2 = 1 → u 2 + v 2 + w 2 = 1

Ou seja, no espaço u v w , temos uma esfera de raio 1 .

Passo 4

Agora vamos ver como fica o volume V

V = ∭ W   d x d y d z = ∭ T J u , v , w d u d v d w

V = ∭ T ( a b c ) d u d v d w   = a b c ∭ T d u d v d w

Mas,

∭ T d u d v d w

É o volume do solído no espaço u v w , ou seja, o volume da esfera de raio 1 , assim

∭ T d u d v d w = 4 π 3

Logo,

V = a b c ⋅ 4 π 3

Resposta

V = a b c ⋅ 4 π 3

Exercício Resolvido #7

UFRJ - Cálculo 3 - PF 2014.2 – 2

Calcule o volume do sólido W limitado pela superfície de equação

x 2 4 + y 2 9 - z 2 = 1

E os planos z = - 1 e z = 2 .

Passo 1

Vamos começar fazendo um esboço disso aí. Temos um hiperboloide de uma folha com simetria em z (a variável que tem sinal diferente) cortado por dois planos:

O hiperboloide tem seção elíptica, porque x e y tem coeficientes diferentes.

Então, W é a região dentro do hiperboloide e entre os planos z = - 1 e z = 2 . Seu volume é dado por

V = ∭ W   d x d y d z

Passo 2

Como a região tem simetria em relação ao eixo z , vamos usar coordenadas cilíndricas com os coeficientes do hiperboloide:

x = 2 r cos ⁡ θ

y = 3 r   s e n   θ

z = z

J = 6 r

Passo 3

Agora, precisamos descobrir como escrever a nossa região. Vamos começar pela variação de r .

x 2 4 + y 2 9 - z 2 = 1 → 2 r cos ⁡ θ 2 4 + 3 r sen ⁡ θ 2 9 - z 2 = 1 →

r 2 cos 2 ⁡ θ + r 2 s e n 2 θ - z 2 = 1

r 2 - z 2 = 1

r = z 2 + 1

Como o raio vai desde r = 0 até o hiperboloide, temos 0 ≤ r ≤ z 2 + 1 .

Como o enunciado já diz, - 1 ≤ z ≤ 2 . Sabemos que 0 ≤ θ ≤ 2 π porque temos uma volta completa em torno de z .

Passo 4

Temos, então

V = ∭ W   d x d y d z = ∫ 0 2 π ∫ - 1 2 ∫ 0 z 2 + 1 6 r d r d z d θ

Agora é só resolver isso aí:

= 6 ∫ 0 2 π ∫ - 1 2 r 2 2 0 z 2 + 1 d z d θ =

= 3 ∫ 0 2 π ∫ - 1 2 z 2 + 1 d z d θ =

= 3 ∫ 0 2 π z 3 3 + z - 1 2 d θ =

= 3 ∫ 0 2 π 8 3 + 2 - - 1 3 - 1 d θ =

= 18 ∫ 0 2 π d θ = 36 π

Resposta

36 π

Exercício Resolvido #8

USP - Cálculo 3 - PSUB 2012 – 1

Calcule ∭ R   x 2 + y 2 9 d x d y d z onde

R = x , y , z ∈ R 3 : x ≥ 0 ,   y ≥ 0 ,   z ≥ 0 ,   x 2 + y 2 9 + z 2 ≤ 1 ,   z ≤ x 2 + y 2 9

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

x 2 + y 2 9 + z 2 = 1   ( e l i p s o i d e )

z = x 2 + y 2 9   ( c o n e )

Então, nós temos um esboço parecido com a figura abaixo.

A região do problema é aquela que está dentro do elipsoide e abaixo do cone contida no primeiro octante.

Passo 2

Como a região é limitada por um elipsoide, vamos utilizar coordenadas esféricas com os coeficientes do elipsoide:

x = ρ   s e n   φ   c o s   θ

y = 3 ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = 3 ρ 2 s e n   φ

Passo 3

Precisamos escrever matematicamente a região de integração. Vamos ver primeiro a variação de ρ :

x 2 + y 2 9 + z 2 = 1 → ρ   s e n   φ   c o s   θ 2 + 3 ρ   s e n   φ   s e n   θ 2 9 + ρ cos ⁡ φ 2 = 1 ∴ ρ = 1

Assim, temos que a variação de ρ é:

0 ≤ ρ ≤ 1

Passo 4

O ângulo φ , como vemos pela figura, varia desde a superfície do cone até π / 2 (lembre-se de que a região está no primeiro octante. Então, vamos fazer a mudança esférica no cone:

ρ cos ⁡ φ = ( ρ   s e n   φ   c o s   θ ) 2 + ( 3 ρ   s e n   φ   s e n   θ ) 2 9

ρ cos ⁡ φ = ρ 2 s e n 2   φ

t g φ = 1

φ = π 4

Assim, a variação de φ é:

π 4 ≤ φ ≤ π 2

Passo 5

Já que temos 1 / 4 de volta em torno do eixo z , 0 ≤ θ ≤ π / 2 (lembra que nossa região se limita ao primeiro octante). Isso nos dá:

W = ρ , θ , φ 0 ≤ θ ≤ π / 2 . ; π / 4 ≤ φ ≤ π / 2 ;   0 ≤ ρ ≤ 1

Passo 6

Vamos agora fazer a substituição esférica na integral:

∭ R   x 2 + y 2 9 d x d y d z =

  ∫ 0 1 ∫ π / 4 π / 2 ∫ 0 π / 2 ( ρ   s e n   φ   c o s   θ ) 2 + ( 3 ρ   s e n   φ   s e n   θ ) 2 9 3 ρ 2 s e n φ   d θ d φ d ρ

= 3 ∫ 0 1 ∫ π / 4 π / 2 ∫ 0 π / 2 ρ 2 s e n 2   φ   ρ 2 s e n φ   d θ d φ d ρ =

= 3 ∫ 0 1 ∫ π / 4 π / 2 ∫ 0 π / 2 ρ 4 s e n 3   φ   d θ d φ d ρ =

Passo 7

Agora vamos integrar em relação a θ :

=   ∫ 0 1 ∫ π / 4 π / 2 ρ 4 s e n 3   φ θ 0 π / 2 d φ d ρ =

= π 2 ∫ 0 1 ∫ π / 4 π / 2 ρ 4 s e n 3   φ d φ d ρ =

Passo 8

Agora em relação a φ :

= π 2 ∫ 0 1 ∫ π / 4 π / 2 ρ 4 s e n 2   φ   s e n   φ d φ d ρ =

= π 2 ∫ 0 1 ∫ π / 4 π / 2 ρ 4 ( 1 - cos 2 ⁡ φ )   s e n   φ d φ d ρ =

= π 2 ∫ 0 1 ∫ π / 4 π / 2 ρ 4 s e n   φ - s e n   φ cos 2 ⁡ φ d φ d ρ =

= π 2 ∫ 0 1 - cos ⁡ φ + cos 3 ⁡ φ π / 4 π / 2 d ρ =

= π 2 ∫ 0 1 0 + 0 - - 2 2 + 2 2 8 d ρ =

= π 2 8 ∫ 0 1 d ρ =

Finalmente:

= π 2 8

Resposta

π 2 8