Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Coordenadas Esféricas

Ver Todos os Exercícios

Teoria

Fala aí, vamos falar de coordenadas esféricas? Vamos começar com a definição:

Definição de Coordenadas Esféricas

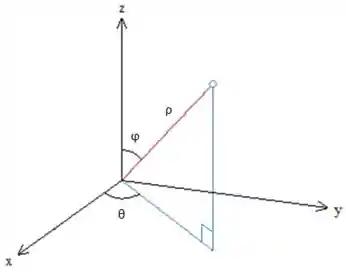
Estamos acostumados a escrever as coordenadas no por exemplo, fornecendo três valores , , e , que junto indicam um ponto para gente. Para definir um ponto em coordenadas esféricas vamos usar três letras gregas, uma delas indicando um comprimento, e duas delas indicando ângulos, olha essa imagem aqui:

Então temos:

  • representando a distância entre o ponto e a origem dos eixos (0,0,0).
  • é o ângulo formado no plano em relação ao eixo
  • é o ângulo formado no plano em relação ao eixo

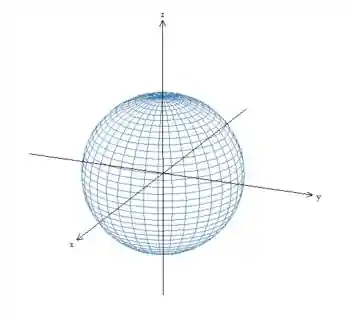
Esse tipo de sistema de coordenadas é muito utilizados para calcular integrais triplas de regiões esféricas. Por exemplo, caso eu queria descrever a equação de uma esfera com raio , basta eu escrever a equação . Como não definimos valores para os ângulos podemos assumir que ambos variam de até :

Gerando o seguinte gráfico:

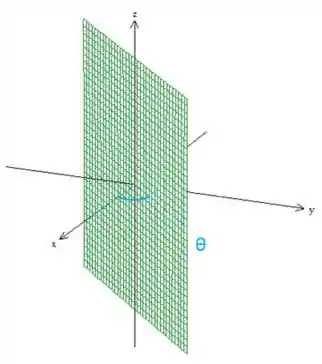
Agora se eu escrevo a equação º, independente de e de . Então eu gero o seguinte plano":

Então tá, já entendemos que podemos desenhar figuras no alterando os valores das nossas variáveis. Agora o que precisamos aprender, e o que cai na sua prova, é como podemos fazer a mudança de variáveis das coordenadas cartesianas para as coordenadas esféricas.

Mudança para coordenadas esféricas

Fazer essa mudança é um processo sempre parecido, mas que envolverá fazer muitas contas. Começaremos calculando o Jacobiano, que pode ser encontrado através das relações da seguinte figura:

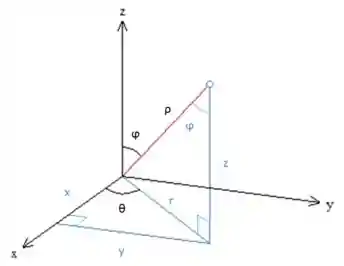
Aqui com um pouco de geometria podemos escrever:

E com isso calcular o Jacobiano:

📢OBS: Caso você não saiba o que é Jacobiano, ou não saiba como calcular o Jacobiano, confere essa página onde explicamos TUDO sobre o Jacobiano: Matriz Jacobiana.

Nosso Jacobiano no nosso exemplo vale:

Esse resultado é valido para casos em que não temos coeficientes nas expressões de , e . O melhor jeito de entender como fazer a mudança de bases das coordenadas cartesianas para as coordenadas esféricas é através de um exemplo, então confere esse vídeo aqui que nossos experts preparam para você!

Exercício

Confere um exercício do nosso tópico de Mudança para Coordenadas Esféricas para você ter certeza que entendeu o conceito!

Mudança para coordenadas esféricas

Exercício

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 957

Calcule ∭ B   e x 2 + y 2 + z 2 3 / 2 d x d y d z , onde B é a bola unitária:

B = { ( x , y , z ) | x 2 + y 2 + z 2 ≤ 1 }

Passo 1

Precisamos escrever matematicamente essa região. Como B é limitada por uma esfera e a função a ser integrada possui termos quadráticos, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Como já vimos, a região de integração passa a ser, então:

B = { ( ρ , θ , φ ) | 0 ≤ ρ ≤ 1 ; 0 ≤ θ ≤ 2 π ; 0 ≤ φ ≤ π }

Passo 2

Vamos agora substituir os intervalos que encontramos na integral iterada. Sabemos que x 2 + y 2 + z 2 = ρ 2 em coordenadas esféricas. Temos, então:

∫ 0 π ∫ 0 2 π ∫ 0 1 e ρ 2 3 / 2 ρ 2 s e n   φ d ρ   d θ   d φ = ∫ 0 π ∫ 0 2 π ∫ 0 1 e ρ 3 ρ 2 s e n   φ d ρ   d θ   d φ =

Passo 3

Fazendo a substituição ρ 3 = u , temos 3 ρ 2 d ρ = d u . A integral passa a ser:

= 1 3 ∫ 0 π ∫ 0 2 π ∫ 0 1 e u s e n   φ d u   d θ   d φ =

= 1 3 ∫ 0 π ∫ 0 2 π s e n   φ e u u = 0 u = 1   d θ   d φ =

= 1 3 ∫ 0 π ∫ 0 2 π s e n   φ ( e - 1 ) d θ   d φ =

Passo 4

Agora, integramos em relação a θ :

= ( e - 1 ) 3 ∫ 0 π s e n   φ   θ θ = 0 θ = 2 π   d φ =

= 2 π ( e - 1 ) 3 ∫ 0 π s e n   φ   d φ =

Passo 5

Finamente, integramos em relação a φ :

= - 2 π ( e - 1 ) 3 cos ⁡ φ 0 π =

= - 2 π e - 1 3 - 1 - - 2 π e - 1 3 =

= 2 π e - 1 3 + 2 π e - 1 3 =

Resposta

4 π e - 1 3

Exercício Resolvido #2

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 957, adaptado.

Utilize coordenadas esféricas para determinar o volume do sólido que se encontra acima do cone z = x 2 + y 2 e dentro da esfera x 2 + y 2 + z 2 = z .

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Completando o quadrado na equação da esfera, temos:

x 2 + y 2 + z 2 - z = 0

x 2 + y 2 + z - 1 2 2 - 1 4 = 0

x 2 + y 2 + z - 1 / 2 2 = 1 4

Uma esfera centrada em ( 0,0 , 1 / 2 ) . Como o cone está expresso na forma z = x 2 + y 2 e sabemos que a raiz deve ser sempre positiva, a parte a que o enunciado se refere é a folha de cima, com z ≥ 0 . Temos, então, essa região da figura:

Passo 2

Temos que V = ∭ W   d V

Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:

x = ρ sen ⁡ φ c o s   θ

y = ρ   sen ⁡ φ sen ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

Passo 3

Precisamos escrever matematicamente a região de integração.

Pela própria figura, já vemos que 0 ≤ θ ≤ 2 π , pois o sólido está em volta do eixo z , fazendo uma volta completa. Os valores de ρ , nós vemos que variam desde a origem ρ = 0 até a superfície da esfera. Vamos, então, fazer a mudança de coordenadas na sua equação:

ρ sen ⁡ φ cos ⁡ θ 2 + ρ sen ⁡ φ sen ⁡ θ 2 + ρ cos ⁡ φ 2 = ρ cos ⁡ φ

ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ + ρ 2 sen 2 ⁡ φ sen 2 ⁡ θ + ρ 2 cos 2 ⁡ φ = ρ cos ⁡ φ

ρ 2 sen 2 ⁡ φ   + ρ 2 cos 2 ⁡ φ = ρ cos ⁡ φ

ρ = cos ⁡ φ

Temos, então, 0 ≤ ρ ≤ cos ⁡ φ

Note que, como a esfera não está centrada na origem, não temos ρ = ( n ú m e r o ) para sua equação, pois a distância dos seus pontos à origem não é constante.

Falta, então, o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , quando φ = 0 até a superfície do cone, então vamos escrever sua equação em coordenadas esféricas:

ρ cos ⁡ φ = ρ sen ⁡ φ cos ⁡ θ 2 + ρ sen ⁡ φ sen ⁡ θ 2

ρ cos ⁡ φ = ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ + ( ρ 2 sen 2 ⁡ φ )   sen 2 ⁡ θ

ρ cos ⁡ φ = ρ 2 sen 2 ⁡ φ   = ρ sen ⁡ φ

sen ⁡ φ = cos ⁡ φ   → tg ⁡ φ = 1   →   φ = π / 4

Portanto, 0 ≤ φ ≤ π / 4 . A região será escrita como:

W = { ( ρ , θ , φ ) | 0 ≤ φ ≤ π / 4 ; 0 ≤ θ ≤ 2 π ;   0 ≤ ρ ≤ cos ⁡ φ   }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada.

∫ 0 π / 4 ∫ 0 2 π ∫ 0 cos ⁡ φ ρ 2 sen ⁡ φ d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π / 4 ∫ 0 2 π ρ 3 3 sen ⁡ φ ρ = 0 ρ = cos ⁡ φ   d θ   d φ =

= 1 3 ∫ 0 π / 4 ∫ 0 2 π cos 3 ⁡ φ sen ⁡ φ d θ   d φ =

Passo 6

Agora, integramos em relação a θ :

= 1 3 ∫ 0 π / 4 ( θ cos 3 ⁡ φ sen ⁡ φ ) θ = 0 θ = 2 π d φ =

= 2 π 3 ∫ 0 π / 4 cos 3 ⁡ φ sen ⁡ φ d φ =

Passo 7

Vamos resolver essa integral aqui rapidinho.

∫ cos 3 ⁡ φ sen ⁡ φ d φ

Repara que temos um seno e um cosseno ao cubo ali, se fizermos

u = cos ⁡ φ

A sua derivada vai estar na integral, então vamos fazer essa substituição

u = cos ⁡ φ → d u = - sen ⁡ φ d φ

A nossa integral vai ficar

∫ cos 3 ⁡ φ sen ⁡ φ d φ = ∫ u 3 - d u = - ∫ u 3 d u

E vamos ter

- ∫ u 3 d u = - u 4 4

Voltando para φ

- u 4 4 = - cos 4 ⁡ φ 4

E assim temos nossa integral.

Passo 8

Voltando para nossa integral vamos ter

2 π 3 ∫ 0 π / 4 cos 3 ⁡ φ sen ⁡ φ d φ =

= 2 π 3 - cos 4 ⁡ φ 4 0 π / 4 = - 2 π 12 cos 4 ⁡ φ φ = 0 φ = π 4

= - π 6 2 2 4 - 1 4 = - π 6 1 4 - 1 =

= - π 6 - 3 4 = π 8

Resposta

π 8

Exercício Resolvido #3

UFRJ, Cálculo III, P1/2012.2, 2

Calcular a integral tripla

J = ∭ W   z   d x d y d z

Onde W é o sólido no primeiro octante limitado pelas superfícies de equações x 2 + y 2 + z 2 = 4 z e z = 3 ( x 2 + y 2 ) , satisfazendo z ≤ 3 ( x 2 + y 2 ) .

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Completando o quadrado na equação da esfera, temos:

x 2 + y 2 + z - 2 2 = 4

Uma esfera centrada em ( 0,0 , 2 ) de raio ρ = 2 . Como o cone está expresso na forma z = 3 ( x 2 + y 2 ) e sabemos que a raiz deve ser sempre positiva, a parte a que o enunciado se refere é a folha de cima, com z ≥ 0 (em vermelho). Tomamos a região que fica abaixo do cone porque a questão pede que z ≤ 3 ( x 2 + y 2 ) .

Como o enunciado pede a região contida no 1º octante ( x ≥ 0   e   y ≥ 0 ) , temos, então:

Passo 2

Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:

x = ρ sen ⁡ φ cos ⁡ θ  

y = ρ sen ⁡ φ sen ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

Passo 3

Precisamos escrever matematicamente a região de integração.

Pela própria figura, já vemos que 0 ≤ θ ≤ π / 2 (o que corresponde ao 1º octante). Os valores de ρ , nós vemos que variam desde a origem ρ = 0 até a superfície da esfera. Vamos, então, fazer a mudança de coordenadas na sua equação:

ρ cos ⁡ θ sen ⁡ φ 2 + ρ sen ⁡ φ sen ⁡ θ 2 + ρ cos ⁡ φ 2 = 4 ρ cos ⁡ φ

ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ + ( ρ 2 sen 2 ⁡ φ )   s e n 2 θ + ρ 2 cos 2 ⁡ φ = 4 ρ cos ⁡ φ

ρ 2 sen 2 ⁡ φ + ρ 2 cos 2 ⁡ φ = 4 ρ cos ⁡ φ

ρ = 4 cos ⁡ φ

Temos, então, 0 ≤ ρ ≤ 4 cos ⁡ φ

Falta, então, o intervalo de φ . Pela figura, vemos que esse ângulo varia desde a superfície do cone até o plano x y , onde temos φ = π / 2 . Vamos, então, escrever a equação desse cone em coordenadas esféricas:

ρ cos ⁡ φ = 3 ρ sen ⁡ φ cos ⁡ θ 2 + 3 ρ sen ⁡ φ sen ⁡ θ 2

ρ cos ⁡ φ = 3 ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ + 3 ( ρ 2 sen 2 ⁡ φ ) sen 2 ⁡ θ

ρ cos ⁡ φ = 3 ρ 2 sen 2 ⁡ φ   = 3 ρ sen ⁡ φ

3 sen ⁡ φ = cos ⁡ φ   → tg ⁡ φ   = 3 / 3     →   φ = π / 6

Portanto, π / 6 ≤ φ ≤ π / 2 . A região será escrita como:

W = { ( ρ , θ , φ ) | 0 ≤ θ ≤ π / 2 ; π / 6 ≤ φ ≤ π / 2 ;   0 ≤ ρ ≤ 4 cos ⁡ φ }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada.

∫ π / 6 π / 2 ∫ 0 π / 2 ∫ 0 4 cos ⁡ φ ( ρ cos ⁡ φ ) ρ 2 sen ⁡ φ   d ρ   d θ   d φ =

= ∫ π / 6 π / 2 ∫ 0 π / 2 ∫ 0 4 cos ⁡ φ ρ 3 sen ⁡ φ cos ⁡ φ   d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ π / 6 π / 2 ∫ 0 π / 2 ρ 4 4 sen ⁡ φ cos ⁡ φ ρ = 0 ρ = 4 cos ⁡ φ   d θ   d φ =

= ∫ π / 6 π / 2 ∫ 0 π / 2 256 cos 4 ⁡ φ 4 sen ⁡ φ cos ⁡ φ   d θ   d φ =

= ∫ π / 6 π / 2 ∫ 0 π / 2 64 cos 5 ⁡ φ sen ⁡ φ   d θ   d φ =

Passo 6

Agora vamos integrar em relação a θ :

= 64 ∫ π / 6 π / 2 θ cos 5 ⁡ φ sen ⁡ φ θ = 0 θ = π / 2   d φ =

= 32 π ∫ π / 6 π / 2 cos 5 ⁡ φ sen ⁡ φ   d φ =

Passo 7

Vamos fazer agora a substituição cos 6 ⁡ φ = u , temos ( - 6 cos 5 ⁡ φ sen ⁡ φ d φ = d u ) e a integral passa a ser:

= 32 π ∫ π / 6 π / 2 - 1 6 d u =

cos ⁡ π / 2 = 0   → u = 0

cos ⁡ π / 6 = 3 2 → u = 27 64

= - 32 6 π - 27 64 =

Resposta

9 π 4

Exercício Resolvido #4

UFRJ, Cálculo III, P1/2012.1, 2

Calcule

J = ∭ W   z 2   d x d y d z

Onde W = { ( x , y , z ) ∈ R 3 | x 2 + y 2 + z 2 ≥ 1 ,   x 2 + y 2 + z - 2 2 ≤ 4   e   z ≥ x 2 + y 2 }

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

Temos uma esfera de raio ρ = 1 centrada na origem, em azul, e outra de raio 2 centrada em ( 0,0 , 2 ) , em verde. Temos a folha superior de um cone (pois a raiz deve ser positiva).

Queremos a região que está fora da esfera de raio 1 (pois o enunciado pede x 2 + y 2 + z 2 ≥ 1 ), dentro da esfera de raio 2 (pois temos x 2 + y 2 + z - 2 2 ≤ 4 ) e, ao mesmo tempo, acima do cone ( z ≥ x 2 + y 2 ). Fazendo esses cortes, teremos então:

Passo 2

Como a região é limitada por duas esferas e um cone, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Passo 3

Precisamos agora escrever matematicamente a região de integração.

Pela própria figura, já vemos que 0 ≤ θ ≤ 2 π (uma volta completa em torno de z ). Os valores de ρ , nós vemos que variam desde a superfície da esfera menor até a da esfera maior. A esfera menor, como está centrada na origem, pode ser escrita como ρ = 1 . Precisamos, então, fazer a mudança de coordenadas na equação da esfera maior:

ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ - 2 2 = 4

ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ - 4 ρ cos ⁡ φ + 4 = 4

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ = 4 ρ cos ⁡ φ

ρ = 4 cos ⁡ φ

Temos, então 1 ≤ ρ ≤ 4 cos ⁡ φ .

Falta agora o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , onde temos φ = 0 até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:

ρ cos ⁡ φ = ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2

ρ cos ⁡ φ = ρ 2 s e n 2 φ cos 2 ⁡ θ + ( ρ 2 s e n 2 φ )   s e n 2 θ

ρ cos ⁡ φ = ρ 2 s e n 2 φ   = ρ   s e n   φ

s e n   φ = cos ⁡ φ   → t g   φ = 1     →   φ = π / 4

Portanto, 0 ≤ φ ≤ π / 4 . A região será escrita como:

W = { ( ρ , θ , φ ) | 0 ≤ θ ≤ 2 π ; 0 ≤ φ ≤ π / 4 ;   1 ≤ ρ ≤ 4 cos ⁡ φ }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada:

∫ 0 π / 4 ∫ 0 2 π ∫ 1 4 cos ⁡ φ ρ cos ⁡ φ 2 ρ 2 s e n   φ   d ρ   d θ   d φ =

= ∫ 0 π / 4 ∫ 0 2 π ∫ 1 4 cos ⁡ φ ρ 4 cos 2 ⁡ φ s e n   φ   d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π / 4 ∫ 0 2 π ρ 5 5 cos 2 ⁡ φ s e n   φ ρ = 1 ρ = 4 cos ⁡ φ   d θ   d φ =

= 1 5 ∫ 0 π / 4 ∫ 0 2 π 4 5 cos 7 ⁡ φ s e n   φ - cos 2 ⁡ φ s e n φ   d θ   d φ =

Passo 6

Agora vamos integrar em relação a θ :

= 1 5 ∫ 0 π / 4 ( 4 5 cos 7 ⁡ φ s e n   φ - cos 2 ⁡ φ s e n φ ) θ θ = 0 θ = 2 π   d φ =

= 2 π 5 ∫ 0 π / 4 4 5 cos 7 ⁡ φ s e n   φ - cos 2 ⁡ φ s e n φ   d φ =

= 2 π 5 ∫ 0 π / 4 4 5 cos 7 ⁡ φ s e n   φ   d φ - ∫ 0 π / 4 cos 2 ⁡ φ s e n φ   d φ =

Passo 7

Vamos calcular separadamente cada integral. Para a 1ª, faremos:

cos 8 ⁡ φ = u

- 8 s e n   φ cos 7 ⁡ φ d φ = d u

cos ⁡ 0 = 1   → u = 1

cos ⁡ π / 4 = 2 2 → u = 1 / 16

∫ 0 π / 4 4 5 cos 7 ⁡ φ s e n   φ   d φ = 4 5 ∫ 1 1 / 16 - 1 8 d u =

= - 128 u 1 1 / 16 = - 8 - 128 = 120

Passo 8

Para a segunda, faremos:

cos 3 ⁡ φ = v

- 3 s e n   φ cos 2 ⁡ φ d φ = d v

cos ⁡ 0 = 1   → v = 1

cos ⁡ π / 4 = 2 2 → v = 2 4

∫ 0 π 4 cos 2 ⁡ φ s e n φ   d φ = ∫ 1 2 4 - 1 3 d v =

= - v 3 1 2 / 4 = - 1 3 2 4 - 1 = 1 3 - 2 12

Passo 9

Substituindo os valores, encontrados, temos:

2 π 5 120 - 1 3 - 2 12 =

Resposta

718 π 15 + 2 π 30

Exercício Resolvido #5

USP - Cálculo 3 - P1 2015 – 3

Calcule a massa do sólido que é parte da bola x 2 + y 2 + z - 2 2 ≤ 4 , acima do cone z = 1 3 ( x 2 + y 2 ) e abaixo do cone z = x 2 + y 2 , com densidade δ x , y , z = z .

Passo 1

O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por δ x , y , z . Nós sabemos que:

d m =   δ x , y , z d V

Onde d m é o diferencial de massa e d V o de volume. Integrando ambos os lados na região W em que o sólido está contido, temos que:

M = ∭ W   δ x , y , z d V

M = ∭ W   z   d x d y d z

Passo 2

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera x 2 + y 2 + z - 2 2 = 4 de raio 2 deslocada da origem em z , ou seja, com centro em ( 0,0 , 2 ) . Temos também dois cones: z = 1 3 ( x 2 + y 2 ) e z = x 2 + y 2 . Para desenhar eles, você precisa notar que o primeiro tem uma abertura maior do que o segundo, pois, pensando em coordenadas cilíndricas, temos z = 1 3 r e z = r (logo, para um mesmo r , o z do primeiro é menor).

Então, desenhando essas três superfícies, temos:

O problema pede o sólido que é parte da bola x 2 + y 2 + z - 2 2 ≤ 4 , está acima do cone z = 1 3 ( x 2 + y 2 ) (de abertura maior) e abaixo do cone z = x 2 + y 2 (de abertura menor).

Cortando, temos isso aqui:

Show?

Passo 3

Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Passo 4

Precisamos escrever matematicamente a região de integração.

O raio varia desde a origem, onde ρ = 0 até a superfície da esfera. Como a esfera não está centrada na origem, precisamos fazer a mudança de coordenadas na sua equação para descobrir a expressão de ρ :

( ρ   s e n   φ   c o s   θ ) 2 + ( ρ   s e n   φ   s e n   θ ) 2 + ρ cos ⁡ φ - 2 2 = 4

ρ 2 s e n 2 φ + ρ 2 cos 2 ⁡ φ - 4 ρ cos ⁡ φ + 4 = 4

ρ 2 - 4 ρ cos ⁡ φ = 0

ρ = 4 cos ⁡ φ

Logo, temos 0 ≤ ρ ≤ 4 cos ⁡ φ .

Como temos uma volta completa em torno do eixo z , temos 0 ≤ θ ≤ 2 π .

E o ângulo φ , como vemos pela figura, varia desde a superfície de um cone até a do outro. Então vamos fazer a mudança esférica nos dois cones:

z = 1 3 ( x 2 + y 2 )

ρ cos ⁡ φ = 1 3 ( ( ρ   s e n   φ   c o s   θ ) 2 + ( ρ   s e n   φ   s e n   θ ) 2 )

ρ cos ⁡ φ = 1 3 ρ 2 s e n 2 φ

ρ cos ⁡ φ = ρ   s e n   φ 1 3

t g   φ = 3

φ = π 3

ρ cos ⁡ φ = ( ρ   s e n   φ   c o s   θ ) 2 + ( ρ   s e n   φ   s e n   θ ) 2

ρ cos ⁡ φ = ρ 2 s e n 2 φ

ρ cos ⁡ φ = ρ   s e n   φ

φ = π 4

Logo,   π / 4 ≤ φ ≤ π / 3 . Assim, temos a região:

W = { ( ρ , θ , φ ) | 0 ≤ θ ≤ 2 π ; π / 4 ≤ φ ≤ π / 3 ;   0 ≤ ρ ≤ 4 cos ⁡ φ ) }

Passo 5

Vamos agora (finalmente) fazer a substituição esférica na integral:

M = ∭ W   z   d x d y d z

= ∫ π / 4 π / 3 ∫ 0 2 π ∫ 0 4 cos ⁡ φ ρ cos ⁡ φ ρ 2 s e n   φ   d ρ d θ d φ =

= ∫ π / 4 π / 3 ∫ 0 2 π ∫ 0 4 cos ⁡ φ ρ 3 s e n   φ cos ⁡ φ   d ρ d θ d φ =

Passo 6

Agora vamos integrar em relação a ρ :

= ∫ π / 4 π / 3 ∫ 0 2 π ρ 4 4 s e n   φ cos ⁡ φ 0 4 cos ⁡ φ d θ d φ =

= 64 ∫ π / 4 π / 3 ∫ 0 2 π s e n   φ cos 5 ⁡ φ d θ d φ =

Passo 7

Agora em relação a θ :

= 128 π ∫ π / 4 π / 3 s e n   φ cos 5 ⁡ φ d φ =

Passo 8

Agora, vamos fazer a substituição:

cos ⁡ φ = u

- s e n   φ   d φ = d u

φ = π 4                 →             u = 2 2

φ = π 3                 →             u = 1 2

Levando isso para a integral, temos:

= - 128 π ∫ 2 / 2 1 / 2 u 5 d u =

= - 128 π u 6 6   2 / 2 1 / 2 =

= - 64 π 3 1 64 - 8 64 =

= 7 π 3

Resposta

7 π 3

Exercício Resolvido #6

UFRJ, Cálculo III, P1/2010.1, 3

Determine o volume do sólido W dado por

W = { ( x , y , z ) ∈ R 3 | x - 1 2 + y 2 + z 2 ≤ 1   e   z ≥ x 2 + y 2 }

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

Temos uma esfera de raio ρ = 1 centrada em ( 1,0 , 0 ) e a folha superior de um cone (pois a raiz deve ser positiva).

Queremos a região que está dentro da esfera de raio 1 (pois o enunciado pede x 2 + y 2 + z 2 ≤ 1 )e, ao mesmo tempo, acima do cone ( z ≥ x 2 + y 2 ). Fazendo esses cortes, teremos então:

Passo 2

Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Passo 3

Precisamos agora escrever matematicamente a região de integração.

Pela própria figura, já vemos que – π / 2 ≤ θ ≤ π / 2 (girando em sentido anti-horário, nós vamos desde a parte negativa do eixo y até a positiva). Os valores de ρ , nós vemos que variam desde a origem até a superfície da esfera., vamos, então, escrevê-la em coordenadas esféricas:

x - 1 2 + y 2 + z 2 = 1   → x 2 + y 2 + z 2 = 2 x

ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 = 2 ρ   s e n   φ   c o s   θ

ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ = 2 ρ   s e n   φ   c o s   θ

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ = 2 ρ   s e n   φ   c o s   θ

ρ = 2   s e n   φ   c o s   θ

Temos, então 0 ≤ ρ ≤ 2   s e n   φ   c o s   θ .

Falta agora o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , onde temos φ = 0 até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:

ρ cos ⁡ φ = ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2

ρ cos ⁡ φ = ρ 2 s e n 2 φ cos 2 ⁡ θ + ( ρ 2 s e n 2 φ )   s e n 2 θ

ρ cos ⁡ φ = ρ 2 s e n 2 φ   = ρ   s e n   φ

s e n   φ = cos ⁡ φ   → t g   φ = 1     →   φ = π / 4

Portanto, 0 ≤ φ ≤ π / 4 . A região será escrita como:

W = { ( ρ , θ , φ ) | – π / 2 ≤ θ ≤ π / 2   ; 0 ≤ φ ≤ π / 4 ;   0 ≤ ρ ≤ 2   s e n   φ   c o s   θ

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada:

∫ 0 π / 4 ∫ - π / 2 π / 2 ∫ 0 2   s e n   φ   c o s   θ ρ 2 s e n   φ   d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π / 4 ∫ - π / 2 π / 2 ρ 3 3 s e n   φ ρ = 0 ρ = 2   s e n   φ   c o s   θ   d θ   d φ =

= 1 3 ∫ 0 π / 4 ∫ - π / 2 π / 2 8   s e n 4 φ cos 3 ⁡ θ   d θ   d φ =

Passo 6

Vamos rearrumar a integral dessa forma:

= 1 3 ∫ 0 π / 4 ∫ - π / 2 π / 2 8   s e n 4 φ 1 - s e n 2 θ cos ⁡ θ   d θ   d φ =

E fazer a substituição s e n   θ = u , cos ⁡ θ d θ = d u :

= 1 3 ∫ 0 π / 4 ∫ - 1 1 8   s e n 4 φ 1 - u 2   d u   d φ =

= 8 3 ∫ 0 π / 4 s e n 4 φ u - u 3 3 u = - 1 u = 1 d φ =

= 8 9 ∫ 0 π / 4 s e n 4 φ 3 u - u 3 u = - 1 u = 1 d φ =

= 8 9 ∫ 0 π / 4 4   s e n 4 φ d φ = 32 9 ∫ 0 π / 4   s e n 4 φ d φ =

Passo 7

Para resolver essa integral, vamos usar a fórmula do arco duplo s e n 2 φ = 1 - cos ⁡ 2 φ 2 :

= 32 9 ∫ 0 π / 4   s e n 2 φ 2 d φ = 32 9 ∫ 0 π / 4   1 - cos ⁡ 2 φ 2 4 d φ =

= 8 9 ∫ 0 π / 4 1 - 2 cos ⁡ 2 φ + cos 2 ⁡ 2 φ d φ =

Usando a fórmula novamente, temos c o s 2 2 φ = 1 + cos ⁡ 4 φ 2 :

= 8 9 ∫ 0 π 4 1 - 2 cos ⁡ 2 φ + 1 + cos ⁡ 4 φ 2 d φ =

= 4 9 ∫ 0 π / 4 2 - 4 cos ⁡ 2 φ + 1 + cos ⁡ 4 φ d φ =

= 4 9 3 φ - 4 s e n 2 φ 2 + s e n 4 φ 4 0 π / 4 =

= 4 9 3 π 4 - 2 =

Resposta

3 π - 8 9

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ