Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 10
10. Obtenha o gráfico de em duas janelas de inspeção distintas, cada uma delas ilustrando uma propriedade diferente de . Identifique cada uma das duas janelas e uma carcteristica do gráfico de que esteja bem exemplificada na janela.
Passo 1
Belezera galera, um gráfico da função pode ser dado como:
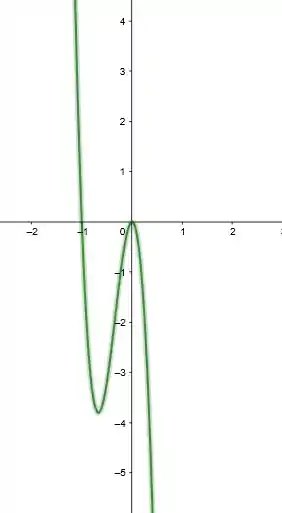
E isso é, analisando o gráfico mais de perto,teríamos a impressão de que ele vai para o e também para de acordo com suas assíntotas.
Passo 2
MAAASSS agora, que em a malandragem, porque nosso gráfico está com a escala de 1 em , vamos trocar para e ver como que fica:
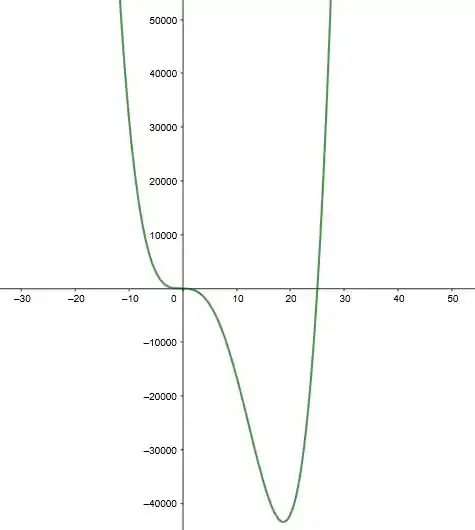
E olha lá o que aconteceu, nosso gráfico na verdade não está indo para o e sim para nos dois sentidos do eixo.
Resposta
Demonstração.
Exercícios de Livros Relacionados
Esboce o gráfico da equação por translação, reflexão, compressão e alongamento do gráfico de y = x 2 , y = x , y = 1 / x , y = x ou y = x 3 de maneira apropriada e, então, use um recurso gráfico para
Esboce o gráfico da equação por translação, reflexão, compressão e alongamento do gráfico de y = x 2 , y = x , y = 1 / x , y = x ou y = x 3 de maneira apropriada e, então, use um recurso gráfico para
Use o Teorema 0.2.3 para determinar se os gráficos têm simetrias em relação ao eixox, ao eixo y ou à origem.(a) x 4 = 2 y 3 + y (b) y = x 3 + x 2 (c) y 2 = x - 5
Use o Teorema 0.2.3 para determinar se os gráficos têm simetrias em relação ao eixox, ao eixo y ou à origem.(a) x = 5 y 2 + 9 (b) x 2 - 2 y 2 = 3 (c) x y = 5
(i) Use um recurso computacional para fazer o gráfico daequação no primeiro quadrante. [Nota: Para isso, resolva a equação parayem termos dex.](ii) Use a simetria para fazer um esboço à mão de todo o