Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 6
6. Uma bola com raio de 15 cm recebe uma camada uniforme de plástico.
- Expresse o volume de plástico como uma função da espessura da camada.
- Qual é o dominio da função volume obtida em (a)?
Passo 1
Show de bicicletinhas meus amores, queremos medir o volume dessa camada uniforme que envolve nossa bola de raio . Podemos fazer um desenho mais ou menos desse momento dessa forma:
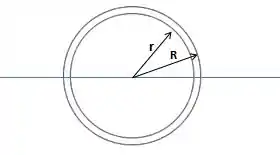
Onde é o raio da esfera antes da camada, e é o raio da esfera depois de envolvida pela camada. A espessura da camada é dada por:
Então:
Passo 2
O volume da bola inicialmente é dado pela expressão:
E o volume da bola após a camada de plástico é:
Dado que :
Portanto, o volume da camada de plástico vai ser dado pela diferença entre o volume final menos o volume inicial:
E abrindo o produto notável , temos:
Substituindo no volume:
Como o enunciado deu pra gente que , podemos substituir esse valor na nossa expressão:
Passo 3
E o dominio dessa função será todos os reais, já que se trata de um polinômio do terceiro grau: