Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 111

111. Dada a integral ∫ d d + 6 x 2 + b x + c d x , onde b, c e d são constantes. Suponha que essa integral seja aproximada pela regra do trapézio com n = k   . (a) Mostre que o erro na aproximação é extamente - 36 k 2   .(b) Qual é o menor valor de k   tal que a aproximação seja exata até uma casa decimal?

Passo 1

O que o enunciado nos pede é para mostrarmos que o erro na aproximação do cálculo de uma integral definida é igual ao valor dado no enunciado. Para isso devemos saber que o erro de uma função que é aproximada pela regra do trapézio é dado por: E ≤ n h 3 12 M a x   f ´ ´ c ,   onde M a x   f ´ ´ c é igual ao valor da 2ª derivada no ponto de máximo da função. Utilizando o conceito de área de um trapézio, o esboço da figura que segue e a fórmula para o erro chegamos ao resultado.

Passo 2

Letra(a)

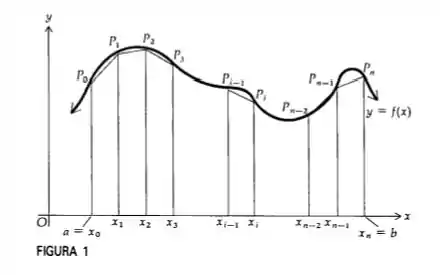
Note que um trapézio tem como área a seguinte equação:

A T R = B + b . h 2 = f a + f a + ∆ x . h 2

Note também que altura depende de quantos trapézios eu fracionei meu intervalo, pois todos trapézios possuem mesma altura.

Logo, h = b - a n tal que n = k pelo enunciado. Então:

h = d + 6 - d k = 6 k

Passo 3

Obtendo o valor da segunda derivada no ponto de máximo da função que está na integral:

f x = x 2 + b x + c

f ´ ´ x = 2 , logo para qualquer valor de x   o valor máximo é 2.

Passo 4

Substituindo as informações obtidas acima na equação do erro temos:

E ≤ n h 3 12 M a x   f ´ ´ c ≤ k . 1 12 6 k 3

e ≤ 6 2 k 2

- 36 k 2 ≤ E ≤ 36 k 2

Passo 5

Letra(b)

Nesse caso o erro deve ser E = 0,1 , logo:

0,1 = 6 2 k 2

k 2 = 6 2 0,1

k = 360

Resposta

  1. Demonstração.
  2. k = 360
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ - 1 1 ( t 3 + 1 ) d t com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 0 3 1 x + 1 d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
A instrução para a integral ∫ 1 2 xd x , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ - 1 1 ( x 2 + 1 )d x , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
A instrução para a integral ∫ 1 2 1 s 2d s , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.