Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 1
1-8. Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico.
1.
Passo 1
Então pessoal, uma equação de parábola em seu formato geral, de acordo com a seção 10.5 do James, é dada da seguinte maneira:
No qual seu foco é dado em e sua diretriz é dada em . Um outro formato é obtido se fizermos a inversa dessa função, ou seja, refleti-la em torno da reta . Se fizermos isso, o formato geral da equação de parábola ficará:
No qual seu foco é dado em e sua diretriz é dada em . No nosso caso temos uma parábola no formato , não é mesmo? Sendo assim, usaremos as informações desse formato, assim como comentado aqui em cima.
Passo 2
Para encontrarmos o vértice de uma parábola, ou seja, o ponto em que ela muda de sentido, precisamos determinar e , no qual significam do vértice e do vértice, respectivamente. As equações são:
Para a equação que nos foi dada temos que: . Logo:
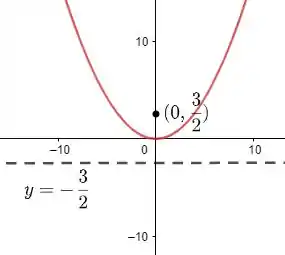
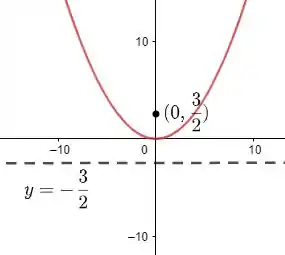
Portanto o vértice será: .
Passo 3
Para determinar o foco e a diretriz temos que encontrar , assim como comentado no passo 1, certo? Se igualarmos a equação que nos foi dada com a equação geral da parábola, teremos:
Sendo assim, a diretriz será: .
Como o foco é dado no ponto , então o foco para essa parábola será: . Por fim, esboçando esse gráfico:
Resposta
