Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 19
19-24. Encontre os vértices, os focos e as assíntotas da hipérbole e esboce seu gráfico.
19.
Passo 1
De acordo com a seção 10.5, desde que a hipérbole não esteja deslocada, são equações de hipérbole:
Dessas duas equações a que se assemelha com a equação que nos foi dada pelo enunciado é o segundo tipo. Para esse segundo tipo a equação da hipérbole apresenta focos em:
Vértices em:
E, por fim, assíntotas em:
A equação que nos foi dada é:
Então disso podemos tirar que: e , tranquilão?!
Passo 2
Beleza, agora já identificamos quem é e , mas falta identificar quem é , não é mesmo? Para uma hipérbole podemos determinar utilizando a seguinte relação:
Substituindo os valores de e , teremos:
Prontinho, agora nosso problema já está praticamente resolvido! Determinamos , e , então é só substituir nas relações comentadas no passo anterior, saca só:
Por fim, esboçando o gráfico, teremos:
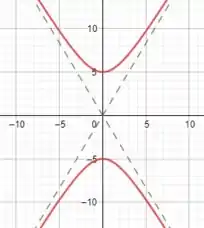
Resposta
