Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 28a
28. Uma massa de 0,25 kg cai, a partir do repouso, em um meio que oferece uma resistência de 0,2|υ|, em que υ está em m/s.(a) Se a massa cai de uma altura de 30 m, encontre sua velocidade ao atingir o solo.(b) Se a massa não pode atingir uma velocidade maior do que 10 m/s, encontre a altura máximada qual ela pode ser largada.(c) Suponha que a força de resistência é k|υ|, onde υ está em m/s e k é constante. Se a massa caide uma altura de 30 m e tem que atingir o solo com uma velocidade menor ou igual a 10 m/s,determine o coeficiente de resistência k necessário
Passo 1
Para resolver essa questão precisamos fazer uma análise das forças em questão
Podemos fazer um pequeno truque aqui
Visto que essa questão quer a velocidade em função da distância, podemos fazer a seguinte manipulação
E olha que ótimo temos em mãos uma equação separável, isso facilita muito nosso trabalho
Para resolver essa integração vamos precisar fazer uma substituição
Assim nossa integral fica da seguinte maneira
Voltando de e continuando nossa solução
Passo 2
Vamos descobrir o valor de C , utilizando os dados de contorno
Com isso nossa função fica
Passo 3
Se queremos saber a velocidade que ela chega ao chão vamos apenas botar os valores e calcular
Vamos precisar ser mais rigorosos com o logaritmo para que ele não fique com argumento negativo. Colocamos para consertar então modulo, para que peguemos a parte positiva. Okay podemos manipular um pouco essa equação e assim obter valores numéricos mais simples
Essa equação não tem um resultado analítico , para resolver vamos precisar fazer uma analise gráfica. Achar os pontos onde intercepta com
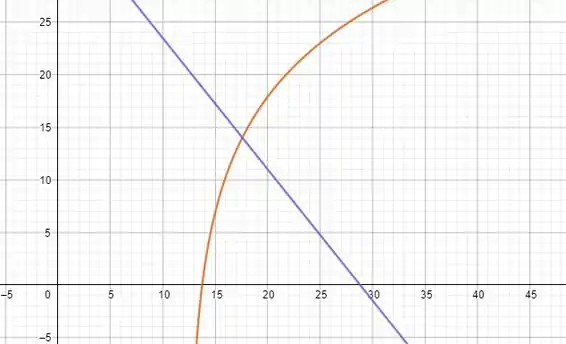
Esse ponto de interseção nos da
Terminamos por aqui. Te vejo na próxima resolução
: )