Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 25a

25. Um corpo de massa m é projetado verticalmente para cima com uma velocidade inicial υ0 emum meio que oferece uma resistência k|υ|, em que k é constante. Não leve em consideraçãovariações na força gravitacional.(a) Encontre a altura máxima xm alcançada pelo corpo e o instante tm no qual essa alturamáxima é atingida.(b) Mostre que, se kυ0/mg tm e xm podem ser expressos como

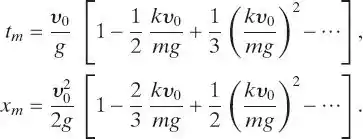
(c) Mostre que a quantidade kυ0/mg é adimensional.

Passo 1

Para resolver essa questão precisamos fazer uma análise das forças em questão

F r =   - F g - F a

m a =   - m g - k v

Podemos fazer um pequeno truque aqui

m d v d t =   - m g - k v

d v d t =   - g - k m v

E olha que ótimo temos em mãos uma equação separável, isso facilita muito nosso trabalho

1 g + k m v d v =   - 1 d t

Vamos integrar em ambos os lados agora

m k ln ⁡ g + k m v =   - t + C

Fazendo umas manipulações podemos escrever nossa função como

g + k m v = C e - t k m

v = m k C e - t k m - g

Passo 2

Vamos descobrir o valor de C , utilizando os dados de contorno

v 0 = v 0

v 0 =   m k C - g  

C = k m v 0 + g

Logo nossa função é

v = m k k m v 0 + g e - t k m - g

Passo 3

Vamos descobrir o tempo necessário para que nosso objeto chegue na altura máxima

v t = 0

0 =   m k k m v 0 + g e - t k m - g

k m v 0 + g e - t k m - g = 0

e - t k m = g k m v 0 + g

- t k m = ln ⁡ g k m v 0 + g

Fazendo umas manipulações podemos escrever nossa equação como

t = m k ln ⁡ k m g v 0 + 1

Passo 4

Agora para encontrar a distancia podemos integrar a nossa função velocidade

d s d t = m k k m v 0 + g e - t k m - g  

s = m k k m v 0 + g - m k e - t k m - g t + s 0

Para descobrir S 0   vamos usar os dados de contorno

S 0 = 0

0 = m k k m v 0 + g - m k - g t + s 0

S 0 =   - m k k m v 0 + g - m k - g t

Com isso nossa função fica

s = m k k m v 0 + g - m k 1 - e - t k m - g t

Para descobrirmos a altura máxima podemos plotar o valor de t em s

S t m =   m k k m v 0 + g - m k 1 - e - m k ln ⁡ k m g v 0 + 1 k m - g m k ln ⁡ k m g v 0 + 1  

Fazendo algumas manipulações podemos escrever essa função como

S t m =   m k k m v 0 + g - m k 1 - k m g v 0 + 1 - g m k ln ⁡ k m g v 0 + 1  

S t m = - m k v 0   - g m k 2   - k m g v 0 - g m k 2 ln ⁡ k m g v 0 + 1

S t m = - g m k 2 - k m g v 0 + ln ⁡ k m g v 0 + 1 + m k v 0     k m g v 0

S t m = - g m k 2 - k m g v 0 + ln ⁡ k m g v 0 + 1 + v 0 2 g  

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

t = m k ln ⁡ k m g v 0 + 1

S t m = - g m k 2 - k m g v 0 + ln ⁡ k m g v 0 + 1 + v 0 2 g  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. Um paraquedista pesando 180 lb (incluindo o equipamento) cai verticalmente de uma altura de5000 pés** e abre o paraquedas depois de 10 s de queda livre. Suponha que a força deresistência do ar, qu
28. Uma massa de 0,25 kg cai, a partir do repouso, em um meio que oferece uma resistência de 0,2|υ|, em que υ está em m/s.(a) Se a massa cai de uma altura de 30 m, encontre sua velocidade ao atingir o
27. Um corpo caindo em um fluido relativamente denso, óleo, por exemplo, está sob a ação de trêsforças (veja a Figura 2.3.5): uma força de resistência R, um empuxo B e seu peso w devido àgravidade. O
28. Uma massa de 0,25 kg cai, a partir do repouso, em um meio que oferece uma resistência de 0,2|υ|, em que υ está em m/s.(a) Se a massa cai de uma altura de 30 m, encontre sua velocidade ao atingir o
27. Um corpo caindo em um fluido relativamente denso, óleo, por exemplo, está sob a ação de trêsforças (veja a Figura 2.3.5): uma força de resistência R, um empuxo B e seu peso w devido àgravidade. O