Exercícios de Modelagens com Fator Integrante - Lista de Exercícios Resolvida

Considere um tanque que possui litros de água pura. Suponha que ele comece a receber produtos químicos, completamente diluídos em água, a uma taxa de litros por hora, e que a concentração desses produtos na água que ali está entrando varia periodicamente com o tempo (medido em horas), de acordo com a fórmula

quilogramas por litro

A solução então é misturada completamente e sai do tanque também à taxa de litros por hora. Determine a quantidade de produtos químicos (em quilogramas) que permanece no tanque após horas.

Lembrete:

Um corpo se move através de um fluido viscoso sob ação de uma força resultante , onde depende da forma do corpo, é a velocidade do corpo e é o coeficiente de viscosidade. Obter a velocidade como função do tempo. Suponha que o movimento seja retilíneo, que a força aplicada seja constante e que

Resolva o circuito RL:

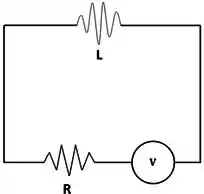
Sabendo que as quedas de voltagem são:

E que a força eletromotriz é:

E com a lei de Kirchoff: ”A soma algébrica de todas as quedas de tensão em torno de qualquer circuito fechado é nula, ou a tensão aplicada em um circuito fechado é igual à soma das quedas de tensão no resto do circuito.”

Considere um tanque que possui litros de água pura. Suponha que ele comece a receber produtos químicos, completamente diluídos em água, a uma taxa de litros por hora, e que a concentração desses produtos na água que ali está entrando varia periodicamente com o tempo (medido em horas), de acordo com a fórmula

quilogramas por litro

A solução então é misturada completamente e sai do tanque também à taxa de litros por hora. Determine a quantidade de produtos químicos (em quilogramas) que permanece no tanque após horas.

Lembrete:

Um tanque contém inicialmente 10 litros de água pura. Injeta-se no tanque uma solução clorada à taxa de , contendo . A solução bem misturada é retirada do tanque à taxa de . A função que representa a quantidade de cloro após minutos é solução do problema com condição inicial:

(a)

(b)

(c)

(d)

(e)

Resolva o problema de valor inicial

Considere o Problema de Valor Inicial (PVI)

1. Encontre um fator integrante que torna a equação do PVI acima exata.

Considere o Problema de Valor Inicial (PVI)

1. Encontre a solução do PVI, dada de forma implícita.

Um tanque contém litros de água pura. Água salgada contendo de sal por litro entra no tanque a uma taxa de litros por minuto. A solução bem misturada é bombeada para fora do tanque na taxa de litros por minuto. Calcule qual a quantidade de sal após 5 minutos.

Um tanque contém de água. Uma solução com concentração salina de é adicionada à taxa de . A solução é mantida misturada e é retirada do tanque na taxa de Se é a quantidade de sal (em quilogramas) após minutos, qual é a equação diferencial que modela essa mistura?

a)

b)

c)

d)

e)

Um tanque contém de água. Uma solução com concentração salina de é adicionada a uma taxa de . A solução é mantida misturada e é retirada do tanque a uma taxa de . Se é a quantidade de sal (em ) após minutos, qual a equação diferencial que modela essa mistura ?

Um tanque possui litros de solução com cloro numa concentração de . Adiciona-se água ao tanque por uma mangueira numa taxa de contendo de cloro e a solução homogênea sai do tanque por um orifício em sua base com vazão de . A quantidade de cloro da solução homogênea no tanque no instante é solução do seguinte problema com condição inicial:

Um tanque inicialmente contém de água pura. No instante, é introduzida no tanque água salgada com uma concentração de a uma velocidade de , e a mistura homogênea sai do tanque a uma velocidade de . Se é a quatidade em , de sal no tanque após minutos, quanto vale ?

3. Este limite não existe

Um tanque possui litros de solução com cloro numa concentração de . Se adicionamos água ao tanque por uma mangueira numa taxa de contendo de cloro e a solução homogênea sai do tanque por um orifício em sua base com vazão de , determine:

1. O volume da solução homogênea no tanque no instante
2. A quantidade de cloro no tanque no instante

Questão 2: Encontre a família de curvas no plano tal que em cada ponto, o coeficiente angular da reta tangente à curva, é a soma das coordenadas deste ponto. Encontre o membro da família que passa pela origem.

Um barco a vela de massa parte do cais com velocidade inicial de em direção à uma ilha distante . O barco é impulsionado pela força do vento e sofre uma resistência da água proporcional à sua velocidade com constante de resistência igual a 2.

Determine a velocidade do barco em qualquer instante.

O barco chegará à ilha? Justifique sua resposta.

6. Uma cultura de bactérias cresce a uma taxa proporcional à quantidade presente. Ao fim de 10 min, cresceu 3%.

a) Determine a constante de proporcionalidade.

6. Uma cultura de bactérias cresce a uma taxa proporcional à quantidade presente. Ao fim de 10 min, cresceu 3%.

b) Quanto tempo levará a cultura para duplicar?

Um tanque contém inicialmente (em ) litros de água pura. Injetam-se no tanque litros/hora de água com sal a uma concentração que varia com o tempo segundo a fórmula

kg/litro (para medido em horas),

e retiram-se litros/hora da mistura resultante (assumida sempre homogênea). A função , que representa a quantidade de sal no tanque ao longo do tempo, é a solução da equação diferencial:

nenhuma das demais alternativas

Resolva a equação

Um tanque de litros de capacidade contém inicialmente litros de água. Quando

, adiciona-se ao tanque uma solução de salmoura com de sal por litro, á razão de

litros por minuto, enquanto a mistura escoa á razão de litros por minuto. Determine:

1. O tempo necessário para que ocorra o transbordamento

Um tanque contém inicialmente litros de água. Derrama-se no tanque água contendo

de , numa razão de . A mistura é mantida homogênea e escoa-se na

mesma razão. Depois de . o processo é interrompido e derrama-se água pura no

tanque à razão de , escoando-se a mistura ainda na mesma razão. Ache a quantidade de sal no tanque depois de (a partir ).

Um tanque de litros de capacidade contém inicialmente litros de água. Quando

, adiciona-se ao tanque uma solução de salmoura com de sal por litro, a razão de

1. litros por minuto, enquanto a mistura escoa a razão de litros por minuto. Determine:

b) A quantidade de sal presente no tanque por ocasião do transbordamento

Resolva o problema de valor inicial

Resolva o problema de valor inicial

Resolva o problema de valor inicial

Resolva o problema de valor inicial

Resolva o problema de valor inicial