Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 37
37. Um paraboloide de revolução é obtido fazendo girar a parábola em torno do eixo x. Ache o volume limitado por um paraboloide de revolução e um plano perpendicular a seu eixo, se o plano estiver a 10cm do vértice e se a seção plana de intersecção for um círculo com um raio de 6cm.
Passo 1
Antes de tudo, vamos esse paraboloide,
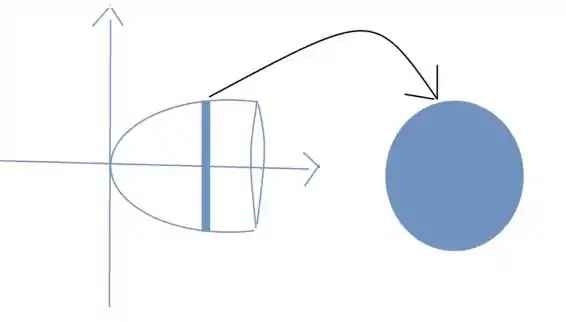
Pegamos a parábola e fatiamos, sendo a fatia um disco de raio y.
Passo 2
E a área do disco será
Passo 3
Antes de continuar, vamos descobrir quem é esse danado do p.
Sabemos que o ponto (10,6) está na parábola, então, colocaremos esse ponto na equação.
Então, a equação da parábola ficará assim:
Passo 4
A integral terá a seguinte cara:
Lembrando que x está variando entre 0 e 10.
Resolvendo a integral:
Resposta
Exercícios de Livros Relacionados
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de A B .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de O C
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de A B .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 2 em torno de O C .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de B C .