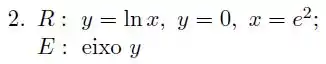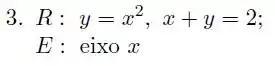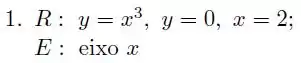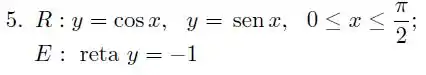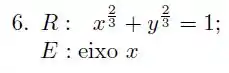Exercícios de Cálculo de Volumes – Discos e Anéis - Lista de Exercícios Resolvida
Questão 1
Seja a região limitada pela curva e pelas retas e . Determine o volume do sólido de revolução gerado pela rotação de em torno, do eixo
Ver solução completaQuestão 2
Determine o volume do sólido obtido pela rotação, em torno da reta , da região
Ver solução completaQuestão 3
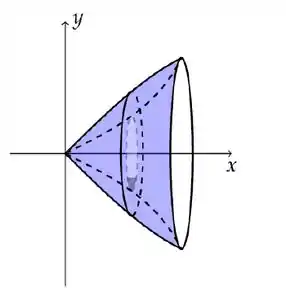
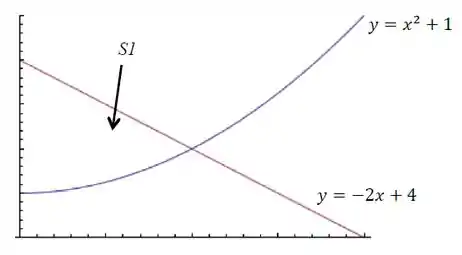
Na figura abaixo, seja o ponto de interseção da curva e a reta , e seja o vértice da parábola . Suponha que a reta passa pelos pontos e .
Calcule o volume gerado pela rotação da região sombreada em torno do eixo-.
Questão 4
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
Calcule o volume do sólido obtido girando a região acima em torno da reta
Ver solução completaQuestão 5
Determine o volume do sólido obtido pela revolução em torno do eixo-, da região limitada pelo gráfico de e no intervalo .
Ver solução completaQuestão 6
Calcule o volume do sólido obtido pela rotação da região em torno do eixo , pelo método que achar mais conveniente.
Ver solução completaQuestão 8
Calcule o volume do sólido de revolução obtido a partir da rotação de
Em torno do eixo .
Ver solução completaQuestão 9
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em torno do eixo .
Ver solução completaQuestão 10
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em torno do eixo .
Ver solução completaQuestão 11
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em torno do eixo .
Ver solução completaQuestão 12
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em torno do eixo .
Ver solução completaQuestão 13
Seja a região delimitada pelas curvas ,
a) Esboce a região
b) Determine a área da região
c) Seja o sólido obtido pela rotação da região ao redor da reta . Expresse o volume por uma ou mais integrais.
d) Calcule o volume de
Ver solução completaQuestão 14
Considere a região R limitada pelas curvas e .
(a) Encontre o valor de c para o qual o sólido obtido pela rotação de R em torno do eixo x tenha volume igual a 8π.
Ver solução completaQuestão 15
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(a) , , .
Ver solução completaQuestão 16
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(d) , , , .
Ver solução completaQuestão 17
Calcular o volume da região delimitada pelas equações , , em torno da reta . Considere = raio interno e =raio externo.
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume inferior a
No cálculo do volume foi obtido um e e um volume inferior a
Ver solução completaQuestão 18
2 – Seja a região do plano limitada pelas curvas e . Seja o sólido de revolução obtido após girar em torno do eixo . Calcule o volume de .
Ver solução completaQuestão 19
Considere a seguinte região do plano: . O volume do sólido obtido pela rotação de A em torno da reta horizontal é igual a:
Ver solução completaQuestão 20
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
b) Calcule o volume do sólido obtido girando a região acima em torno da reta
Ver solução completaQuestão 21
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
c) Calcule o volume do sólido obtido girando a região acima em torno da reta
Ver solução completaQuestão 22
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(c) , .
Ver solução completaQuestão 23
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
d) da reta , usando o método do anel.
Ver solução completaQuestão 24
Um objeto é esculpido a partir de um tronco cilíndrico de madeira maciça com diâmetro de metros e comprimento de metros. O objeto tem a forma do sólido de revolução obtido pela rotação, em torno do eixo , da região limitada pela curva , , e pelo eixo . Calcule o volume de madeira desperdiçado.
Ver solução completaQuestão 25
Considere a região do plano delimitada pela curva de equação e pela reta (eixo ).
- Calcule o volume do sólido gerado pela rotação de em torno da reta (eixo );
- Escreva uma integral que corresponda ao volume do sólido gerado pela rotação de em torno da reta . Não precisa calcular a integral.
Questão 26
Considere a região limitada pelas curvas
Determine o volume do sólido obtido pela rotação de em torno do eixo .
Ver solução completaQuestão 27
Calcular o volume da região delimitada pelas equações , , em torno da reta . Considere = raio interno e =raio externo.
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume inferior a
No cálculo do volume foi obtido um e e um volume inferior a
Ver solução completaQuestão 28
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
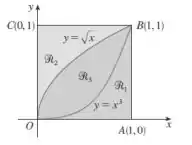
- ao longo de BC
Questão 29
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Questão 30
Calcule o volume do sólido obtido pela rotação da região em torno do eixo , pelo método que achar mais conveniente.
Ver solução completaQuestão 31
Considere a região delimitada pelas retas , , e .
- Esboce a região .
- Escreva uma integral, ou uma soma de integras, que represente(m) o volume do sólido de revolução obtido pela rotação da região ao redor da reta .
- Calcule o volume.
Questão 32
Seja a região do plano limitada superiormente pelo gráfico de e inferiormente pelo eixo , com .
Determine o volume do sólido obtido pela revolução da região em torno do eixo .
Ver solução completaQuestão 33
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Questão 34
Considere a região limitada pelas curvas e no intervalo .
- Esboce a região
- Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Questão 35
Calcule o volume do sólido obtido pela rotação em torno do eixo , da região delimitada pelos gráficos das funções:
Ver solução completaQuestão 36
Calcule o volume do sólido obtido pela rotação em torno do eixo , da região delimitada pelos gráficos das funções:
Ver solução completaQuestão 37
Calcule o volume do sólido obtido pela rotação em torno do eixo , da região delimitada pelos gráficos das funções:
Ver solução completaQuestão 38
Seja A a região limitada pelas curvas e . Seja o sólido gerado pela rotação da região A em torno da reta cujo volume é igual . O valor de é quanto?
Ver solução completaQuestão 39
Encontre a região do sólido quando a região limitada por , , e é girado em torno do eixo.
Ver solução completaQuestão 40
Um tronco de pirâmide com base quadrada de lado , topo quadrado de lado e altura . O que acontece se O que acontece se
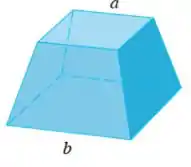
Questão 41
Seja a região limitada pelas curvas e .
- Esboce a região .
- Encontre o volume do sólido de revolução gerado quando é girado ao redor da reta .
Questão 42
Faça um esboço da região do plano limitada pelas curvas e e pelas retas e . Expresse as grandezas abaixo utilizando integrais. Não é preciso calcular as integrais.
- A área de ;
- O volume do sólido de revolução obtido pela rotação de em torno do eixo .
Questão 43
Calcule o volume da esfera de raio usando dos métodos que vimos na aula
Ver solução completaQuestão 44
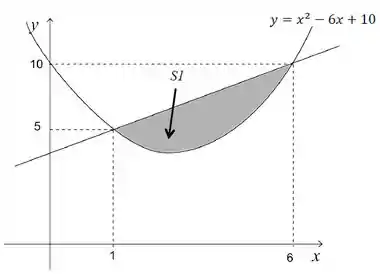
Com base na figura abaixo, determine a área da região , delimitada por , e ; e determine o volume do sólido gerado pela revolução de em torno do eixo .
Questão 45
Com base na figura abaixo, determine a área da região ; e determine o volume do sólido gerado pela revolução de em torno do eixo .
Questão 46
Questão 3:
Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo .
- Esboce abaixo a região plana .
- Utilizando o método que preferir, escreva o volume de como uma integral ou como uma soma de integrais.
- Calcule o volume de .
Obs.: Neste item não é necessário calcular o volume.
Questão 47
Questão 3: Seja
- Esboce a região do plano compreendida pelo gráfico de e o .
- Encontre o volume do sólido obtido pela revolução de em torno do eixo .
(Use uma integral imprópria adequada!)
Ver solução completaQuestão 48
Questão 5) Considere a região limitada pelas curvas e no intervalo . Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Ver solução completaQuestão 49
5) Calcule o volume do sólido de revolução obtido ao rotacionar em torno do eixo a região delimitada pela curva e a reta
Ver solução completaQuestão 50
Q01V) Encontre o volume do sólido obtido pela rotação da região entre as curvas , , e em torno da reta .
Ver solução completaQuestão 51
Determine o volume do sólido obtido pela rotação, em torno do eixo , da região , situada no primeiro quadrante, limitada pelas retas e e pelas curvas e .
Ver solução completaQuestão 52
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Questão 53
Considere a região limitada pelas curvas de equações dadas. Aplicando o método dos discos circulares, calcule o volume do sólido obtido pela rotação da região em torno do eixo dado:
Ver solução completaQuestão 54
Seja uma função contínua. Sabendo-se que o volume do sólido obtido girando o gráfico de em torno do eixo entre e é para todo , encontre a expressão de quando .
Ver solução completaQuestão 55
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
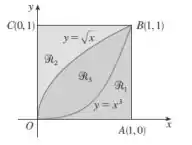
- ao longo de OA
Questão 56
4. Seja a região do plano delimitada pelas curvas , e . Determine o volume do sólido de revolução obtido da rotação de em torno da reta .
Ver solução completaQuestão 57
3. Sera a região limitada pela curva e pelas retas , e . Faça um esboço de e calcule o volume gerado pela rotação de em torno do eixo .
Ver solução completaQuestão 58
Determine o volume do sólido S obtido pela rotação em torno do eixo da região delimitada pelas retas ; ; e pelos gráficos das funções e .
Ver solução completaQuestão 59
Calcule o volume do sólido produzido pela rotação de
ao redor do eixo .
Ver solução completaQuestão 60
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
d)
Ver solução completaQuestão 61
- Calcule o volume do sólido gerado pela rotação, em torno do eixo x, do conjunto de todos os pares tais que e .
- Esboce no mesmo plano os gráficos das polares e , calculando a área da interseção entre elas.
Ver solução completaQuestão 62
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
c)
Ver solução completaQuestão 63
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
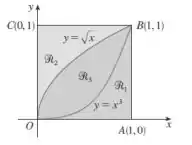
- ao longo de OC
Questão 64
A região sob o gráfico de no intervalo é girado em torno do eixo . Encontre o volume do sólido gerado.
Ver solução completaQuestão 65
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
e)
Ver solução completaQuestão 66
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
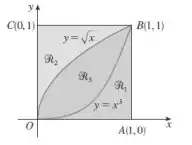
- ao longo de AO.
Questão 67
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
A região do primeiro quadrante delimitada pelos eixos de coordenadas, pela reta e pela curva
Ver solução completaQuestão 68
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completaQuestão 69
Divida uma pizza circular de de diâmetro através de cortes paralelos de maneira que cada uma das três partes tenha a mesma área
Ver solução completaQuestão 70
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completaQuestão 71
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas em torno de
Ver solução completaQuestão 72
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completa
Questão 73
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região do primeiro quadrante limitada à esquerda pelo círculo , à direita pela reta e superiormente pela reta .
Ver solução completaQuestão 74
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
do eixo , usando o método do anel.
Ver solução completaQuestão 75
Determine o volume do sólido obtido pela rotação da região, no segundo quadrante, limitada pela curva , inferiormente pelo eixo e à esquerda pela reta , em torno da reta .
Ver solução completaQuestão 76
Seja R a região limitada pelas curvas e . Seja S o sólido obtido pela rotação da região R em torno de cujo volume é igual a V. O valor de é quanto?
Ver solução completaQuestão 77
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
da reta , usando o método do anel.
Ver solução completaQuestão 78
Seja o sólido comum a duas esferas, cada qual com raio , cujos centros distam entre si. O volume de é
a)
b)
c)
d)
e)
Ver solução completaQuestão 79
a) Considere os parboloides
e
Determine a equação da projeção no plano da curva interseção dos paraboloides. Esboce também esta projeção.
b) Calcule o volume da região espacial
c) Encontre a posição do centroide da região indicada no item 1b.
Ver solução completaQuestão 80
Calcule o volume de uma calota esférica de altura , , de uma esfera de raio .
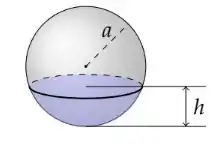
Questão 81
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completaQuestão 84
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completaQuestão 85
Cada integral representa o volume de um solido de revolução. Descreva a região que foi rotacionada e o eixo de rotação.
b.
Ver solução completaQuestão 86
Cada integral representa o volume de um sólido de revolução. Descreva a região que foi rotacionada e o eixo de rotação.
d)
Ver solução completaQuestão 87
Cada integral representa o volume de um sólido de revolução. Descreva a região que foi rotacionada e o eixo de rotação.
c)
Ver solução completaQuestão 88
Um objeto é esculpido a partir de um tronco cilíndrico de madeira maciça com diâmetro de metros e comprimento de metros. O objeto tem a forma do sólido de revolução obtido pela rotação, em torno do eixo , da região limitada pela curva , e pelo eixo . Calcule o volume de madeira desperdiçado.
Ver solução completaQuestão 89
Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
c. 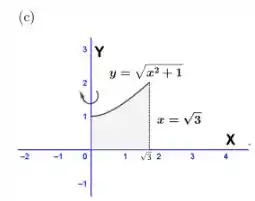
Questão 90
Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
d. 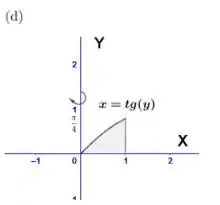
Questão 91
Calcule o volume do sólido de revolução obtido girando-se em torno do eixo a região delimitada pelo eixo , o gráfico de e as retas e .
Ver solução completaQuestão 94
- Calcule o volume do sólido gerado pela rotação, em torno do eixo x, do conjunto de todos os pares tais que e .
- Esboce no mesmo plano os gráficos das polares e , calculando a área da interseção entre elas.
Ver solução completaQuestão 95
1 – Calcule o volume do solido de revolução obtido pelo giro da região limitada por , , e em torno do eixo .
Ver solução completaQuestão 96
Q01V) Responda às perguntas abaixo no espaço adequado no seu caderno de respostas. As soluções devem ser sucintas e a resposta final deve estar destacada do restante da solução.
- A integral representa o volume de um sólido de resvolução. Descreva o sólido
Questão 97
Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
b. 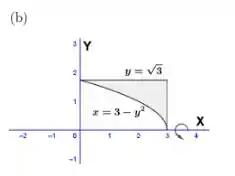
Questão 98
Um fabricante de móveis em madeira produz pés de apoio para móveis a partir de blocos de madeira que serão torneados por uma serra de fita que segue o traçado de uma curva determinada por , de até .
Os pés de apoio são obtidos quando a região sob a curva é girada em torno do eixo . Encontre o volume de cada pé de apoio produzido por este método.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 99
Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
a. 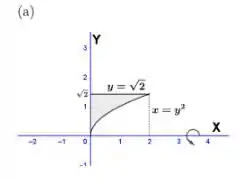
Questão 100
Seja A a região determinada por
Seja o sólido gerado pela rotação de em torno do eixo cujo volume é igual a V. O valor de vale quanto?
Ver solução completaQuestão 101
Seja a região limitada pelas curvas e .
(a) Esboce e calcule a sua área.
(b) Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Ver solução completaQuestão 102
Calcule o volume do sólido de revolução obtido pela rotação do semicírculo:
Em torno da reta .
Ver solução completaQuestão 103
2 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
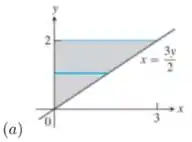
Questão 104
1 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
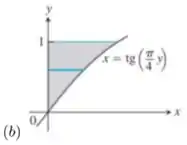
Questão 105
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
b) ,
Ver solução completaQuestão 106
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
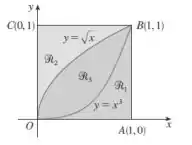
- ao longo de OC
Questão 107
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
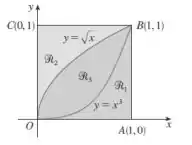
- ao longo de AB
Questão 108
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
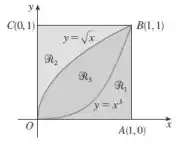
- ao longo de AB.
Questão 109
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região do primeiro quadrante limitada superiormente pela parábola , inferiormente pelo eixo e à direita pela reta .
Ver solução completaQuestão 110
Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
Ver solução completaQuestão 111
Considera a região
Determine o volume do sólido obtido pela rotação da região em torno do eixo .
Ver solução completaQuestão 112
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
f)
Ver solução completaQuestão 113
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
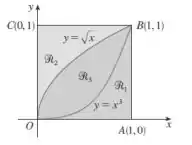
- ao longo de OA
Questão 114
Determine o volume do sólido obtido pela revolução em torno do eixo-, da região limitada pelo gráfico de e no intervalo .
Ver solução completaQuestão 117
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Questão 118
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Questão 119
Considere a seguinte região do plano: . O volume do sólido obtido pela rotação de A em torno da reta horizontal é igual a:
Ver solução completaQuestão 120
Seja a região limitada do plano, que é delimitada pelos gráficos das curvas e , consideradas para valores .
a) Esboce a região , indicando os pontos de interseção das curvas
b) Calcule o volume do sólido obtido ao girar a região em torno da reta
Ver solução completaQuestão 121
Considere a região R limitada pelas curvas e .
(b) Para c = 4, encontre de modo que o sólido obtido pela rotação de R em torno da reta tenha volume igual a 8π.
Ver solução completaQuestão 122
(a) Seja
Calcule o volume do sólido obtido pela rotação de em torno da reta .
(b) Calcule a área da região formada pelos pontos tais que está entre
Ver solução completaQuestão 123
Considere as regiões e definidas a seguir.
é a região do primeiro quadrante limitada pela curva , pelo eixo e pela reta .
é a região limitada pela curva , pelo eixo e pela reta .
Sem calcular as integrais, faça o que se pede a continuação.
- Faça o esboço de e de .
- Escreva uma integral, ou uma soma de integrais, que expresse a área da região .
- Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno do eixo .
- Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno da reta .
Questão 124
Calcule o volume do sólido gerado pela rotação da região delimitada pelos gráficos de e e pelas retas verticais e , girando em torno da reta .
Resposta:
Ver solução completaQuestão 125
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(e) , , , .
Ver solução completaQuestão 126
Determine o volume do sólido obtido pela rotação da região, no primeiro quadrante, limitada superiormente pela curva , inferiormente pelo eixo e à direita pela reta , em torno da reta
Ver solução completaQuestão 127
Esboce e calcule o volume do sólido descrito.
a) Uma calota de altura , de uma esfera de raio .
Ver solução completaQuestão 128
Calcule o volume do sólido obtido pela rotação em torno do eixo do conjunto:
Ver solução completaQuestão 129
Considere a região limitada pela reta e pela curva no intervalo . Esboce a região e calcule o volume do sólido gerado pela rotação de em torno do eixo .
Ver solução completaQuestão 130
A região destacada na figura abaixo é delimitada pelas funções e .
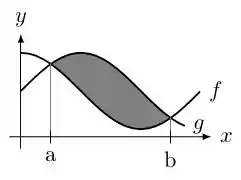
Sabemos que
O volume do sólido de revolução obtido girando em torno do eixo é:
- .
- .
- .
- .
Questão 131
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(b) , .
Ver solução completaQuestão 132
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região delimitada pelo triângulo de vértices em e .
Ver solução completaQuestão 133
Seja a região delimitada pelas curvas .
- Esboce a região .
- Escreva as integrais que determinam o volume do sólido obtido pela rotação da região acima ao redor da reta pelo método das cascas cilíndricas e pelo método dos discos.
- Calcule o volume pedido.
Questão 134
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
ao redor da reta
Ver solução completaQuestão 135
Seja a região que está entre as curvas e no intervalo . Determine o volume do sólido obtido ao rotacionarmos em torno da reta .
Ver solução completaQuestão 136
Calcule o volume do sólido gerado pela rotação da região delimitada pelos gráficos de e e pelas retas verticais e , girando em torno da reta .
Resposta:
Ver solução completaQuestão 138
Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo .
- Esboce a região plana
- Utilizando o método que preferir, escreva o volume de como uma integral
- Calcule o volume de
Questão 139
Calcule o volume do sólido delimitado pelas superfícies a seguir e acima das respectivas regiões do
Ver solução completaQuestão 141
Calcule o volume do sólido cuja base é o semicírculo , , e cujas secções perpendiculares ao eixo são triângulos equiláteros.
Ver solução completaQuestão 142
Determine o volume do sólido de revolução obtido pela rotação, em torno do eixo , da região plana delimitada pelas curvas e , com .
Ver solução completaQuestão 143
Determine o volume do sólido situado entre os planos perpendiculares ao eixo em e , e cujas seções perpendiculares ao eixo são discos circulares com diâmetros que vão do eixo à parábola .
Ver solução completaQuestão 144
Seja S o toro gerado pela rotação do círculo ao redor do eixo y. Construa as integrais que representam o volume do S, pelo método das seções transversais e pelo método das cascas cilíndricas.
Ver solução completaQuestão 145
Calcule o volume do sólido delimitado pelas superfícies a seguir e acima das respectivas regiões do
Ver solução completaQuestão 146
1 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
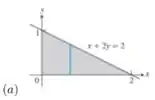
Questão 147
1 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
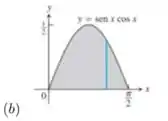
Questão 148
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
ao redor da reta .
Ver solução completaQuestão 149
Determine o volume do sólido tal que:
A base de é um círculo de raio , e as seções transversais perpendiculares à um eixo da base são quadrados.
Ver solução completaQuestão 150
Determine o volume do sólido tal que:
é uma calota de uma esfera de raio e altura .
Ver solução completaQuestão 151
Determine o volume do sólido tal que:
A base de é a região parabólica , e as seções transversais perpendiculares ao eixo são triângulos equiláteros, com um lado na base.
Ver solução completaQuestão 152
Determine o volume do sólido tal que:
A base de é a região limitada pela parábola e pelo eixo , e as seções transversais perpendiculares ao eixo são triângulos isósceles com altura igual à base.
Ver solução completaQuestão 153
Determine o volume do sólido tal que:
é um tetraedro com três faces perpendiculares entre si e três arestas perpendiculares entre si com comprimentos de e .
Ver solução completaQuestão 154
Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em todo do eixo .
Ver solução completaQuestão 155
Determine o volume do sólido tal que:
S é uma pirâmide regular com altura e base quadrada de lado .
Ver solução completaQuestão 156
1) Seja a região plana dada pelo esboço abaixo:
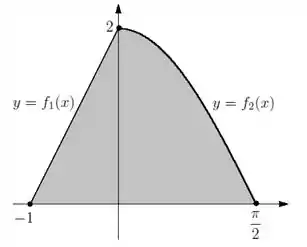
Onde e são funções tais que:
- O gráfico de é uma reta que passa pelos pontos e .
- , onde são constantes reais
Responda:
- Determine a expressão de e
- Seja o sólido de revolução obtido pela rotação da região em torno do eixo . Utilizando o método que preferir, escreva o volume de como uma integral ou uma soma de integrais.
- Calcule o volume de pelo método que preferir.
Questão 157
Seja Calcule o volume do sólido obtido pela rotação de em torno da reta .
Ver solução completaQuestão 158
Q01III) Responda às perguntas abaixo no espaço adequado no seu caderno de respostas. As soluções devem ser sucintas e a resposta final deve estar destacada do restante da solução.
- Seja a região do plano limitada pela parábola e pelo gráfico de . Escreva (mas não calcule!) a integral que representa o volume do sólido obtido rotacionando-se ao redor do eixo .
Questão 159
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Questão 160
Calcule o volume do sólido obtido pela rotação em torno do eixo da região delimitada pela curva e a reta .
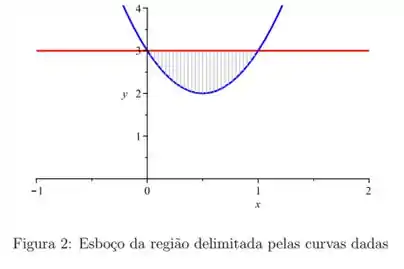
Questão 161
3) Considere a região do plano delimitada superiormente por e inferiormente pelo segmento de reta conectando os pontos do plano e . O volume do sólido obtido girando a região em torno do eixo é:
Questão 162
Considere a função onde . Seja o sólido obtido pela rotação do gráfico de em torno do eixo . O volume de é:
Questão 163
Sejam e funções dadas por
𝑒 considere a região plana descrita abaixo:
Seja o sólido gerado pela rotação da região em torno do eixo
a) Esboce a região plana
b) Escreva o volume de utilizando o Método de Discos ou método de cascas ciníndricas.
Obs: Neste item não é necessário calcular o volume.
Ver solução completaQuestão 164
Considere a região plana
a) Esboce a região plana .
b) Assinale uma das opções abaixo e escreva o volume de utilizando integrais.
[ ] Método de Discos: o volume será escrito através de uma soma de 3 integrais.
[ ] Método de Cascas Cilíndricas: o volume será escrito através de uma única integral.
c) Calcule o volume de .
Ver solução completaQuestão 165
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Questão 166
A região sob o gráfico de no intervalo é girado em torno do eixo. Encontre o volume do sólido gerado.
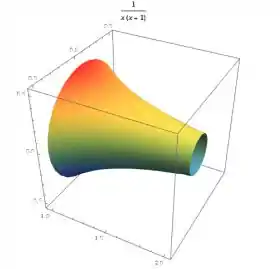
Questão 168
Dada a figura abaixo ache o volume do sólido gerado rotacionando a região indicada em torno da reta especificada:
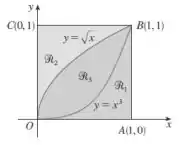
- ao longo de OC
Questão 169
Seja a região ilimitada no plano definida por:
Calcule o volume do sólido de revolução obtido girando em torno do eixo-x.
Ver solução completa