47-48. Use um recurso computacional para gerar os gráficos de e no intervalo indicado; use os gráficos para estimar as coordenadas dos pontos de inflexão de , os intervalos nos quais é côncava para cima ou para baixo e os intervalos nos quais é crescente ou decrescente. Verifique suas estimativas fazendo o gráfico de .
47.
Passo 1
Então galera, o enunciado nos pede várias coisas, sendo assim vamos tomar cuidado para não embaralhar todos os dados, ok? Temos que nossa função é a seguinte:
Primeiramente temos que descobrir e . Derivando, teremos:
Pela segunda vez:
Ok, encontramos nossas derivadas! Agora plotando as derivadas teremos:
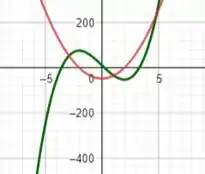
Vale ressaltar que só queremos analisar no intervalo de , beleza? Então bora continuar!
Passo 2
Agora o que temos que encontrar são os pontos de inflexão da função. De acordo com o que vimos na literatura em questão, para encontrarmos isso devemos igualar a nossa derivada segunda a zero, isto é:
Ademais, para determinarmos os intervalos em que a concavidade de é para cima ou para baixo basta analisarmos as desigualdades de para quando é maior que zero e para quando é menor do que zero. A concavidade de está para cima quando:
Como a função está limitada, tem concavidade para cima em e em . Por fim, a concavidade de está para baixo quando:
Como a função está limitada, tem concavidade para baixo em .
Passo 3
Para finalizar nossa análise (amém), basta determinarmos os intervalos em que a função é crescente e decrescente. Parecido com o que fizemos com a concavidade, agora temos que utilizar a derivada primeira, ou seja, , e não mais . A função é crescente quando:
Resolvendo essa equação do terceiro grau teremos que é crescente em e . A função é decrescente quando:
Resolvendo essa equação teremos que é decrescente em e . E está aí nossa análise completa, pessoal!
Resposta
Pontos de inflexão: ;
Concavidade para cima: e em ;
Concavidade para baixo: ;
Intervalo crescente: e ;
Intervalo decrescente: e .