Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.6 - Ex. 41
Ache, com aproximação de 1 grau, as medidas dos ângulos internos do triângulo formado pelas retas que têm equação , e .
Passo 1
Inicialmente vamos traçar as retas no plano cartesiano e fazer o esboço do triângulo. Para esboçar as retas basta substituir dois valores quaisquer de em cada uma das retas. Assim temos:
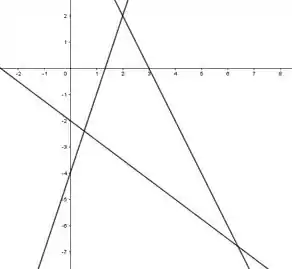
Passo 2
Vamos escrever a equação de cada reta na forma reduzida:
Passo 3
Trataremos por , e . Vamos determinar o ângulo entre cada par de retas.
◦
◦
◦
Resposta
Portanto, os ângulos internos do triângulo formado pelas retas e são 45◦, 108◦ e 27◦.
Exercícios de Livros Relacionados
No exercício a seguir é dado um dos valores de s e nx , cos x e t gx . Determine os outros dois valores quando x está no intervalo especificado. s e nx =- 1 2 ,x ∈ [π ,3 π 2]
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? c o s( x -π 2 )
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? c o sx + 2 π 3 - 2
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? s e n ( x 2 )
No exercício a seguir é dado um dos valores de s e nx , cos x e t gx . Determine os outros dois valores quando x está no intervalo especificado. t gx = 2 ,x ∈ [π , π 2]