Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 41
Ache a área limitada por (a) o laço da limaçon e (b) a parte externa da limaçon.
Passo 1
Para entender melhor a questão é bom ter uma ideia de como é o gráfico da limaçon.
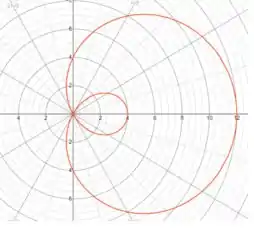
A região que a questão pede para obter a área é a parte fora do laço e dentro da linha externa do limaçon.
Passo 2
Note que, o laço do limaçon compreende os ângulos entre . Desse modo, temos duas integrais para o cálculo da área.
Mas, observe que a área compreendida entre é igual a área compreendida entre . Com isso, o cálculo resume em apenas uma integral.
Passo 3
Sabendo que a área de uma região é dada por:
.
Aplicando na região dada pela questão, temos:
A =
Para resolver a integral do cosseno ao quadrado basta fazer uma identidade trigonométrica.
A = = 142.11
Resposta
A = 142.11 u.a
Exercícios de Livros Relacionados
Nos exercícios de 47 a 56 , calcular a área limitada pela curva dada.
Nos exercícios de 39 a 46 , encontrar a integral que dá o comprimento total da curva dada.
Encontrar a área interior ao círculo r = 6 c o s θ e exterior a r = 2 ( 1 + c o s θ ) .
Nos exercícios de 47 a 56 , calcular a área limitada pela curva dada.
Encontrar a área da intersecção entre r = 2 a c o s θ e r = 2 a s e n θ .