Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 58

Encontrar a área interior ao círculo r = 6 c o s θ e exterior a r = 2 ( 1 + c o s θ ) .

Passo 1

Sabendo que a equação que define a área de uma curva é dada por:

A = 1 2 ∫ θ 0 θ 1 f θ 2 d θ

Se torna necessário definir o intervalo de integração necessário. Para tanto, como a área de interesse é a intersecção entre as duas curvas, é de interesse encontrar os pontos nos quais elas se interceptam.

As curvas se interceptam no ponto em que ambas possuem o mesmo valor, ou seja:

6 c o s θ = 2 + 2 c o s θ

4 c o s θ = 2 → c o s θ = 1 2

∴ θ = π 3

Isso é possível observar no desenho a seguir:

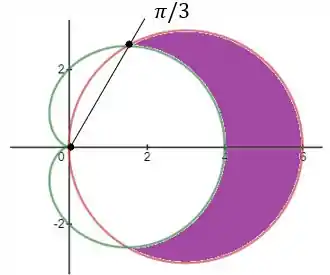
Assim, pode-se calcular a área desejada a partir da subtração das áreas das duas curvas neste trecho.

Passo 2

Logo, a área será dada por:

A = ∫ 0 π / 3 6 c o s θ 2 - 2 + 2 c o s θ 2 d θ

Então:

A = ∫ 0 π / 3 36 c o s 2 θ - 4 + 8 c o s θ + 4 c o s 2 θ d θ

A = ∫ 0 π / 3 3 2 c o s 2 θ - 4 + 8 c o s θ d θ

Passo 3

Logo, lembrando da identidade trigonométrica:

c o s 2 n x = 1 + cos ⁡ 2 n x 2

Tem-se:

A = ∫ 0 π / 3 32 1 + cos ⁡ 2 θ 2 - 4 + 8 c o s θ d θ

A = ∫ 0 π / 3 1 2 + 16 cos ⁡ 2 θ - 8 c o s θ d θ

Resolvendo as integrais:

A = 12 θ + 16 s e n 2 θ 2 - 8 s e n θ π / 3   0

E substituindo os limites de integração:

A = 12 π 3 + 8 s e n 2 π 3 - 8 s e n π 3

Logo:

A = 4 π + 8 3 2 - 8 3 2 = 4 π   u . a .

Resposta

4 π   u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe as retas e seções cônicas nos Exercícios 65-74. r = 1 1 + 2 co s ⁡ θ
Esboce os círculos nos Exercícios 53-56. Dê coordenadas polares para seus centros e identifique seus raios. r = - 8 s en ⁡ θ
Esboce as retas nos Exercícios 45-48 e encontre equações cartesianas para elas. r cos ⁡ θ + 3 π 4 = 1
Esboce as retas nos Exercícios 45-48 e encontre equações cartesianas para elas. r cos ⁡ θ + π 3 = 2
Desenhe as retas e seções cônicas nos Exercícios 65-74. r = 4 sen ⁡ θ