Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.

A seguir damos um esboço do gráfico de nesse intervalo:

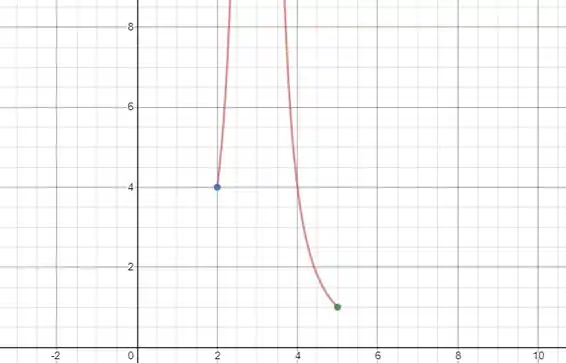
Observe que quando , a função explode para tanto pela direita quanto pela esquerda:

Assim, a função não tem máximo absoluto nesse intervalo, já que cresce indefinidamente até . O mínimo deve ser atingido em um dos extremos do intervalo, já que ele é fechado. Note que , de modo que o mínimo ocorre em .