Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 54
. (a) ache a excentricidade; (b) identifique a cônica; (c) escreva a equação da diretriz que corresponde ao foco na origem; (d) faça um esboço da curva.
Passo 1
Para uma melhor visualização da excentricidade divide-se a equação por 3. Desse modo,
A equação geral é dada por:
Passo 2
Portando a excentricidade é .
Passo 3
Com isso, e sabendo que , então a cônica é uma elipse.
Passo 4
Desse modo, comparando a equação da questão com a equação geral, temos que, . Por meio disso, e sabendo que a equação da diretriz é dada por:
Temos,
Passo 5
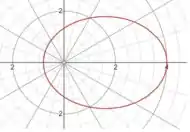
Sabendo que a cônica é uma elipse e tem o sinal negativo, ou seja, ela é mais voltada para a direita, o esboço do gráfico é dado por:
Resposta
Exercícios de Livros Relacionados
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. 1 , 0
Demarcar o seguinte ponto no sistema de coordenadas polares e encontrar suas coordenadas cartesianas. - 3 , π 3
Encontrar um par de coordenadas polares do seguinte ponto: 1,1
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. 4 , 5 π 8
Assinalar o ponto dado em coordenadas polares e depois escrever as coordenadas polares para o mesmo ponto, tal que: r tenha sinal contrário θ tenha sinal contrário 4 , 5 π 6