Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 4b
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares.
Passo 1
O ponto é determinado pelo par ordenado , onde representa a distância entre a origem e o ponto , e representa a medida, em radianos, do ângulo orientado de forma horária ou anti-horária .
Assim, para o ponto dado, temos que e , orientado de forma anti-horária.
Passo 2
As coordenadas polares podem ser transformadas em coordenadas cartesianas pela seguinte substituição:
Esses resultados podem ser concluídos pela definição de seno e cosseno. Observe a figura abaixo:
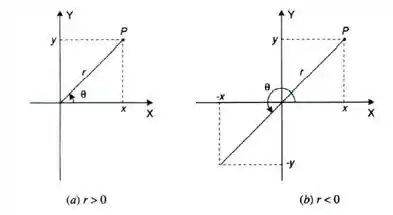
No passo anterior já determinamos que e . Substituindo os valores, temos:
Resposta
Exercícios de Livros Relacionados
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com r0 e outro com r0 . (a) ( 2 ,π 3 ) (b) ( 1 ,- 3 π 4 ) (c) ( - 1 ,π 2
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com r0 e outro com r0 . 1 ,7 π 4 - 3 ,π 6 1 , - 1
As coordenadas cartesianas de um ponto são dadas. (i)Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . (ii) Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . ( 3 3 , 3 )( 1
As coordenadas cartesianas de um ponto são dadas. (i)Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . (ii) Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . ( 2 ,- 2 ) ( -
Marque o ponto cujas coordenadas polares são dadas. A seguir encontre as coordenadas cartesianas no ponto. ( 1 ,π ) ( 2 ,- 2 π 3 ) ( - 2 ,3 π 4 )