Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 48

Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.

Passo 1

Vamos seguir um passo a passo tranquilo pra resolver esses problemas, da mesma forma que o livro faz nos exemplos 3 e 4 desta seção.

Determinar a derivada da função.
Fazer e depois encontrar os valores de para os quais não existe.
Achar os valores de que satisfazem as proposições acima e estão dentro do intervalo especificado.
Dos valores encontrados, o menor vai ser o mínimo absoluto e o maior será o máximo absoluto do intervalo.
Esboçar o gráfico utilizando os valores de máximo e mínimo que temos.

Vamo devagarinho que dá bom!

Passo 2

A derivada da vai ficar:

Passo 3

No nosso caso, não precisamos nos preocupar com os casos onde não existe, já que o seno está definido para todo valor de . Vamos fazer

Ou seja:

Ficaremos com os múltiplos inteiros de dentro do argumento do seno, que são os pontos onde o seno zera. Ou seja:

Onde .

E daí temos que:

Passo 4

Agora vamos considerar o intervalo que estamos analisando:

Precisamos que esteja dentro desse conjunto e também satisfaça a equação em função de que encontramos acima. Se fizermos

Está dentro do nosso intervalo, então é um ponto crítico!

Para

Que já está fora do nosso intervalo. Então só teremos ponto crítico no interior do intervalo, que é: .

Passo 5

Fazendo

Passo 6

Agora podemos fazer um esboço mais fiél do gráfico da função com essa informação. A nossa função tem a cara de um cosseno com amplitude , mas apenas no intervalo que a questão nos dá.

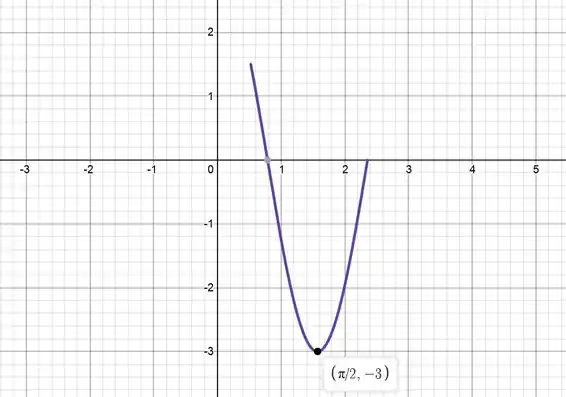
Passo 7

Do gráfico dá pra ver que o ponto de máximo absoluto nesse intervalo é o valor da função no limite inferior do intervalo estipulado. Ou seja, nosso máximo absoluto está em