Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 33
Ache o volume do sólido gerado pela rotação da região do Exercício 32 em torno do eixo y.
Passo 1
No Exercício 32 a região era limitada pelo gráfico de , pelo eixo y e pela reta 6, pela imagem:
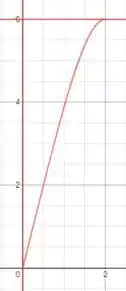
A região está entre as três linhas vermelhas na figura. Usaremos a equação do volume por invólucro cilíndrico, para fazermos a integral e a rotação dessa região:
Passo 2
Como o enunciado nos pede para fazer uma rotação em torno do eixo y, não precisaremos deslocar o valor de x para ajustar o integrando na equação acima. Mas como a região está acima da curva, nossa função será a subtração da reta horizontal por essa curva:
Os limites de integração serão dados pelo valor de x no eixo y, ou seja, , e o valor máximo que x pode assumir na curva .
E a integral do volume ficará:
Passo 3
Reescrevendo a integral acima:
Integrando termo a termo:
Substituindo os limites de integração: