Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 35
O que acontece com o gráfico da equação à medida que varia?
Passo 1
Falaaa... beleza??
Nessa questão vamos analisar o gráfico da equação:
À medida que varia.
Pra isso vamos substituir alguns valores no e plotar o gráfio.
Como é um gráfico complexo, podemos usar algum recurso computacional pra plotar.
Podemos escolher alguns valores de que sejam meio aleatórios, mas de forma estratégica, né? Então podemos escolher valores iguais em módulo (pra todo , vamos escolher também).
Passo 2
A questão pede para analisarmos o comportamento do gráfico da curva conforme varia. A seguir fazemos os plots para vários valores de :
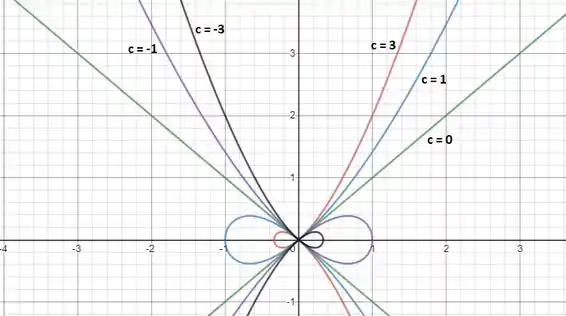
Para , temos duas retas: . Já para , temos um laço à esquerda do eixo e esse laço diminui conforme aumenta. Por outro lado, para , o laço passa para à direita do eixo e também diminui conforme aumenta!
Portante, conforme varia para números diferentes de , é formado um laço que tem a sua área reduziza conforme o módulo de aumenta.
Resposta
Conforme varia para números diferentes de , é formado um laço que tem a sua área reduziza conforme o módulo de aumenta.