Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 34
As curvas com equações
são chamadas curvas ponta de bala. Faça o gráfico de algumas dessas curvas para entender o porquê de seu nome. O que acontece quando cresce?
Passo 1
A questão pede para esboçarmos o gráfico de para diferentes valores de .
Dessa forma, vou plotar aqui a função usando , , e para ver como é o comportamento da função e por que ela é conhecida como ponta de bala.
Passo 2
Plotando a função com os escolhidos, temos o seguinte gráfico:
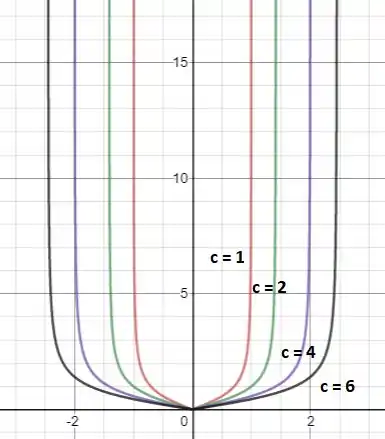
Podemos perceber que a medida que cresce a função vai aumentando ficando cada vez mais gorda, ocupando mais espaço.
Podemos ainda dizer que o domínio (conjunto de valores possíveis para ) da função aumenta a medida que aumenta. Olha só.
Para , a função fica:
E como não podemos ter uma raíz negativa e nem uma divisão por zero, precisa estar entre e .
Para , a função fica:
E da mesma forma, teremos agora que precisa estar entre e .
E assim vai para cada .
Passo 3
Por fim, por que a função se chama ponta de bala. Aí fica da sua interpretação.
Se você considerar bala como o doce bala, realmente ela parece a ponta de uma bala embrulhada.Agora se você considerar bala como o projétil bala, ela também parece uma bala perfurando um alvo.
Como disse, vai da imaginação de cada um.
Resposta
A função vai ficando “gorda” e seu domínio vai aumentando a medida que aumenta.