Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 11
Analise a função trigonométrica no intervalo especificado, enunciando onde é crescente, decrescente, côncava para cima e côncava para baixo e dando as coordenadas de todos os pontos de inflexão. Confirme se seus resultados são consistentes com o gráfico gerado por um recurso.
Passo 1
O primeiro passo que precisamos saber, para determinar a derivada da função:
Essa função zera quando :
A função é crescente quando a primeira derivada é positiva, quando :
Isso acontece quando estamos no intervalo de .
Dentro desse intervalo, a função está sempre crescendo.
- A função é decrescente quando a primeira derivada é negativa, quando:
E quando isso acontece? No intervalo de menos infinito até o zero da função :.
Dentro desse intervalo, a função está sempre decrescendo.
Passo 2
Para os próximos passos vamos calcular a segunda derivada.
Essa função zera quando:
Quando a segunda derivada é positiva, a concavidade é para cima onde . Isso acontece quando:e
Os demais valores fora do intervalo, tem concavidade para baixo onde . Isso acontece quando: e .
O ponto de inflexão é nas raízes onde a segunda derivada é nula, em.
Todos esses valores podem ser comprovados com análise gráfica de:
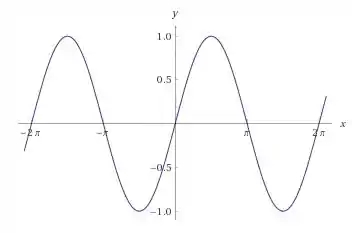
Resposta
Ei, a resposta está no passo a passo :)