Seja:

Encontre se .

Fala povo, tudo ok? Ó só, essa questão parece complicada, mas nota o seguinte, toda função e sua inversão tem domínio e contradomínio funcionando da seguinte forma:

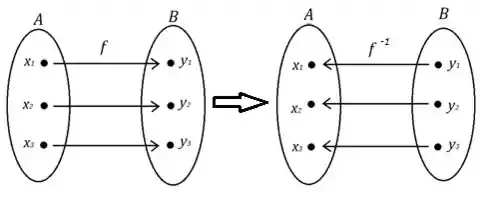
Onde é o domínio de , mas imagem de e é a imagem de , mas o domínio de . Po galera, quando dizemos que:

Estamos na verdade dizendo que é um elemento da imagem da inversa, isto é, do conjunto ! E portanto, ele é um elemento do domínio de . Pra saber com qual elemento de ele se relaciona basta fazermos:

Calculando:

E ta na mão galera, se:

Então pela definição de função inversa: