Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.4 - Ex. 34
Após o álcool ser completamente absorvido pelo corpo, ele é metabolizado com uma meia vida de cerca de 1,5 horas. Suponha que você tenha bebido 3 drinques alcoólicos e uma hora depois, à meia noite, sua concentração de álcool no sangue (CAS) é .
a) Encontre o decaimento exponencial que modela sua CAS horas após meia noite.
b) Faça um gráfico do seu CAS e use-o para determinar quando você pode dirigir para casa se o limite legal é de .
Passo 1
Fala aí! tudo certinho? 😊
Nesse problema temos que obter o decaimento exponencial da função em relação ao tempo e a partir desse gráfico obter o tempo quando é .
Parece complicado? 👀
Mas calma que vou te ajudar no passo a passo. Vem comigo!
Passo 2
Primeiramente, vamos mostrar como é a função de meia vida.
Ela é uma função exponencial do tipo:
Onde representa o valor inicial da concentração de álcool no sangue , a base da potência é igual a , por se tratar da meia vida, e o expoente representa o tempo que demora para que a concentração de álcool caia pela metade.
Pelo enunciado podemos ver que esse tempo será de Assim, a função que modela nosso problema será:
Perfeito, já temos nossa função! 😁
Passo 3
Agora vamos responder cada um dos itens pedidos.
a) Quando deu meia noite, sua concentração de álcool no sangue (CAS) é 0,6 mg/mL. Este valor é a nossa referência, de acordo com o enunciado.
Então:
Então, a equação do decaimento será:
Show, função pronta!
Passo 4
Agora a letra
b) O gráfico do decaimento vai ter esta cara, e o tempo que demora para chegarmos à concentração de pode ser marcada diretamente no gráfico. Veja:
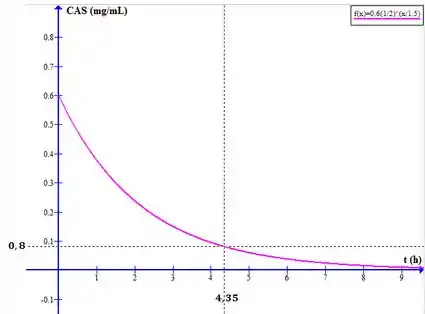
Também podemos ver que para a atingir , podemos usar a equação:
Mostrando que o gráfico está certinho
E aí! o que achou? Responde Aí! 😎