Assinalar o ponto dado em coordenadas polares e depois escrever as coordenadas polares para o mesmo ponto, tal que:
- tenha sinal contrário
- tenha sinal contrário
Passo 1
O ponto é determinado pelo par ordenado , onde representa a distância entre a origem e o ponto , e representa a medida, em radianos, do ângulo orientado de forma horária ou anti-horária .
Assim, para o ponto dado, temos que e , orientado de forma anti-horária.
Logo, graficamente em coordenadas polares temos:
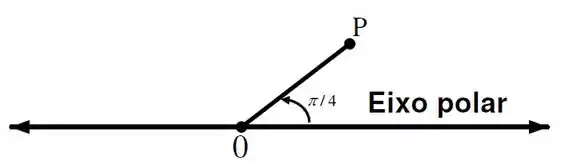
Passo 2
- Para que tenha sinal trocado, ficaríamos com , contudo este ponto não possui a mesma localização do nosso inicial. Logo precisamos deslocar nosso ângulo a fim de que os pontos se coincidam no mesmo lugar do plano polar.
- Para que tenha sinal trocado, ficaríamos com , contudo este ponto não possui a mesma localização do nosso inicial. Logo precisamos deslocar nosso ângulo a fim de que os pontos se coincidam no mesmo lugar do plano polar.
A mudança de sinal em deslocou nosso ponto em , ou seja, unidades. Assim, precisamos somar no nosso ângulo a fim de que o ponto volte para o mesmo lugar no plano. Temos que:
Assim, podemos escrever o mesmo ponto como:
Passo 3
A mudança de sinal em deslocou nosso ponto em no sentido anti-horário, ou seja, unidades. Assim, precisamos girar no sentido horário nosso ângulo a fim de que o ponto volte para o mesmo lugar no plano. Girar no sentido horário implica em sinal negativo.
Assim, podemos escrever o mesmo ponto como:
Resposta
Ei, a resposta está no passo a passo :)