Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.3 - Ex. 5

Encontre as coordenadas cartesianas dos pontos do Exercício 1.

Passo 1

Olá pessoal! Vem comigo.

Como já sabemos o sistemas de coordenadas polares e cartesianas estão relacionados pelas seguinte equações:

Do Exercício 1, temos os seguintes dados:

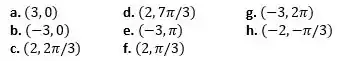
  • Para o item a.:

    • r = 3 θ = 0

    Logo:

    x = 3 cos ⁡ 0 = 3

    y = 3 sen ⁡ 0 = 0

    Então 3 ,   0 .

  • Para o item b.:

    • r = - 3 θ = 0      

    Logo:

    x = - 3 cos ⁡ 0 = - 3

    y = - 3 sen ⁡ 0 = 0

    Então - 3 ,   0 .

    Passo 2

  • Para o item c.:

    • r = 2     θ = 2 π 3

    Logo:

    x = 2 cos ⁡ 2 π 3 = - 1

    y = 2 sen ⁡ 2 π 3 = 3

    Então - 1 ,   3 .

  • Para o item d.:

    • r = 2     θ = 7 π 3

    Logo:

    x = 2 cos ⁡ 7 π 3 = 1

    y = 2 sen ⁡ 7 π 3 = 3

    Então 1 ,   3 .

    Passo 3

  • Para o item e.:

    • r = - 3 θ = π      

    Logo:

    x = - 3 cos ⁡ π = 3

    y = - 3 sen ⁡ π = 0

    Então 3 ,   0 .

  • Para o item f.:

    • r = 2 θ = π 3

    Logo:

    x = 2 cos ⁡ π 3 = 1

    y = 2 sen ⁡ π 3 = 3

    Então 1 ,   3 .

    Passo 4

  • Para o item g.:

    • r = - 3 θ = 2 π      

    Logo:

    x = - 3 cos ⁡ 2 π = - 3

    y = - 3 sen ⁡ 2 π = 0

    Então - 3 ,   0 .

  • Para o item h.:

r = - 2 θ = - π 3

Logo:

x = - 2 cos ⁡ - π 3 = - 1

y = - 2 sen ⁡ - π 3 = 3

Então - 1 ,   3 .

Tchau pessoal.

Resposta

  1. 3 ,   0
  2. - 3 ,   0
  3. - 1 ,   3
  4. 1 ,   3
  5. 3 ,   0
  6. 1 ,   3
  7. - 3 ,   0
  8. - 1 ,   3

Exercícios de Livros Relacionados

Os Exercícios 63-68 fornecem equações para seções cônicas e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada curva será deslocada. Encontre uma equação para
Os Exercícios 63-68 fornecem equações para seções cônicas e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada curva será deslocada. Encontre uma equação para
Os Exercícios 63-68 fornecem equações para seções cônicas e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada curva será deslocada. Encontre uma equação para
Encontre uma equação polar na forma r cos ⁡ θ - θ 0 = r 0 para cada uma das retas nos Exercícios 49-52. 3 x - y = 1
Desenhe as retas e seções cônicas nos Exercícios 65-74. r = 8 4 + cos ⁡ θ