Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 4

Em cada parte, gere o gráfico da função f com um recurso gráfico computacional e determine se f é injetora.

a )   f x = x 3 - 3 x + 2

b )   f x = x 3 - 3 x 2 + 3 x - 1

Passo 1

Fala povo, tudo tranquilo? Bora lá! A ideia aqui vai ser traçar retas horizontais distintas no gráfico dessas funções. Se nenhuma reta horizontal tocar o gráfico duas vezes, a função será injetora. Ou ainda, em outras palavras, se existir uma reta horizontal que toque a função duas ou mais vezes, a função não será injetora. Bora testar?

Passo 2

Letra a)

f x = x 3 - 3 x + 2

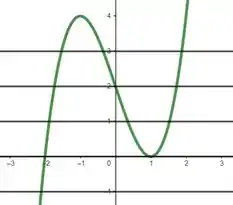
Vemos pelo gráfico e pela natureza dessa função que vão existir infinitas retas horizontais capazes de cruzar o gráfico duas vezes, logo a função não é injetora!

Passo 3

Letra b)

f x = x 3 - 3 x 2 + 3 x - 1

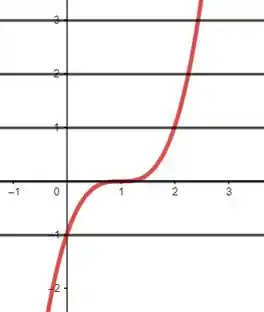
Vemos pelo gráfico e pela natureza dessa função que nenhuma reta horizontal é capaz de cruzar o gráfico mais de uma vez, logo a função é injetora!

Resposta

  1. Não Injetora
  2. Injetora
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dado que y = t g - 1 ( - 2 ) , ache o valor exato de cada uma das funções:11. a) s e n( y )
9. Faça o exercício 7 se x = s e n - 1 ( - 1 3 ) .7. d) s e c( x )
Dado que x = c o s - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:8. d) s e c( x )
Dado que x = c o s - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:8. b) t g( x )
Dado que y = t g - 1 ( - 2 ) , ache o valor exato de cada uma das funções:11. c) c o t g( y )