Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 26
Enfocando conceitos
Esboce o gráfico de uma função que é injetora em embora não crescente em e não decrescente em .
Passo 1
Eita, complicou! Antes de mais nada, vamos lembrar que uma função injetora é uma função que cada está unicamente associado a um único . Portanto a função abaixo não é injetora:
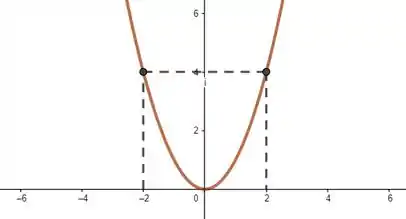
Mas a abaixo é:
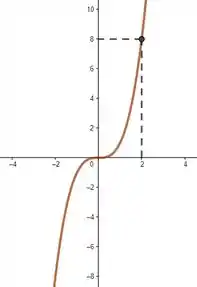
E olha só, a função acima é estritamente crescente em . Já sabemos que ela não serve porque não é isso que o enunciado quer, o que enrola um pouco nossa vida hehehe mas só um pouco, porque toda função estritamente crescente ou decrescente é automaticamente injetora. Então se pudesse, já teríamos matado a questão. O que fazer agora?
Passo 2
Bem galera, se não posso fazer funções estritamente crescentes e nem decrescentes porque a questão não deixou e também não posso fazer funções que cresçam pra depois de crescer ou vice versa porque isso tornaria elas injetoras, o que fazer? Bem, uma boa ideia é pegar uma função que tenda a um valor para pelo menos um dos infinitos!
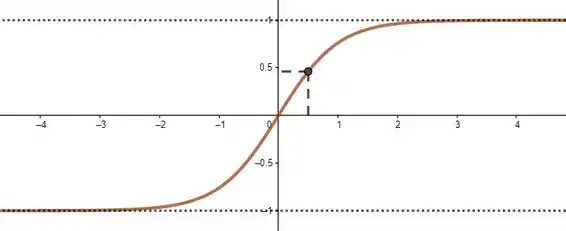
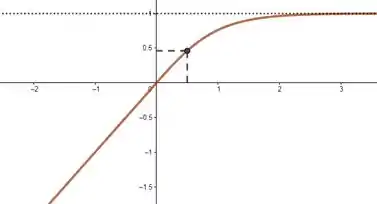
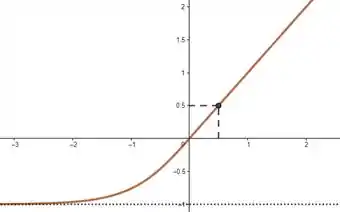
E olha só! Nesse exemplo aí ainda fizemos a função tender a valores distintos pros dois infinitos. Se é infinitamente grande e negativo, a função tá cada vez mais perto de . Se é infinitamente grande e positivo, a função tá cada vez mais perto de . Se a função nunca assume valores maiores que e nem menores que , então ela não é estritamente crescente! E como podemos ver, não há nenhuma reta horizontal que corte o gráfico duas vezes! Só por curiosidade, olha só exemplos em que um só dos infinitos está tendendo a :
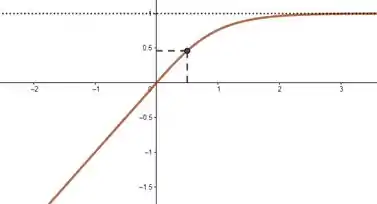
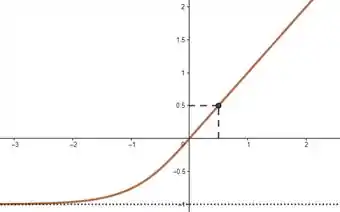
Resposta
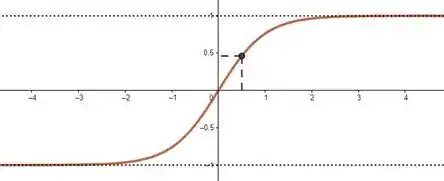
Para fazer uma função injetora que não é estritamente crescente nem decrescente podemos escolher uma função estritamente (de)crescente e transformar a curva de pelo menos um dos infinitos em uma curva que tende a um valor. No exemplo acima, isso foi feito com os dois infinitos. Outros exemplos:
