Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 7
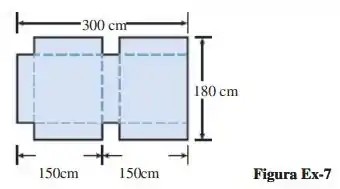
7. Uma caixa fechada deve ser feita de um pedaço de papelão com 180cm por 300 cm, tirando fora quatro quadrados de mesmo tamanho (veja a figura abaixo), dobrando ao longo das retas tracejadas e encaixando para dentro as duas abas da tampa.
- Encontre uma fórmula que expresse o volume da caixa como uma função do comprimento dos lados dos quadrados cortados.
- Encontre uma desigualdade que especifique o dominio da função em (a).
- Use o gráfico da função volume para estimar as dimensões da caixa com o maior volume.
Passo 1
Belezuras galera, o desenho da caixa é esse dai:
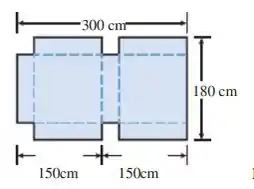
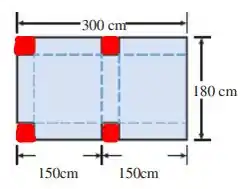
Queremos encontrar o volume dela em função dos lados dos quadradinhos cortados, esses quadradinho bem desenhados aqui:
Passo 2
Dado que:
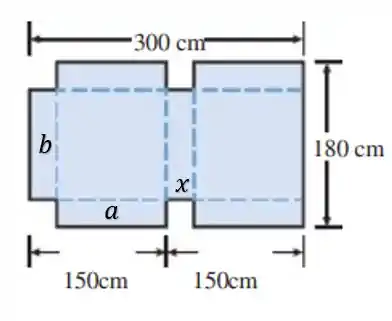
O Volume será dado por:
MAAAS, podemos colocar e em função de , saca só:
Logo o volume será:
Passo 3
E o dominio da função será para todosos valores que não tornem o volume negativo, logo
Resposta
Exercícios de Livros Relacionados
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta19. Uma curva que cruza o eixo x em dois pontos distintos não pode ser o gráfico de uma função.
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta21. A imagem da função valor absoluto é o conjunto de todos os números reais positivos
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta20. O domínio natural de uma função real definida por uma fórmula consiste em todos os números reais com os quais a fórmula fo
Determine se a afirmação dada é verdadeira ou falsa. Explique sua respostaSe g x = 1 / f ( x ) , então o domínio de g consiste em todos os números reais x com os quais f x ≠ 0