Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.Exercícios Práticos - Ex. 47

Um cálculo direto mostra que.

∫ 0 π   2   s e n 2 x   d x = π

Quão próximo desse valor você chega usando a regra do trapézio com n = 6   ? E a regra de Simpson com n = 6 ? Experimente e descubra.

Passo 1

Primeiro, vamos utilizar o método dos Trapézios, ok?

Vamos descobrir o tamanho dos subintervalos, certo?

Δ x = b - a n = π - 0 6   ⟹ π 6 ;

Então, Δ x 2 = π 12

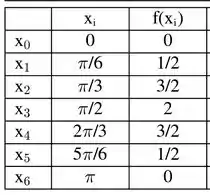
Usando a regra do trapézio,

T = π 12 0 + 2 ⋅ 1 2 + 2 ⋅ 3 2 + 2 ⋅ 2 + 2 ⋅ 3 2 + 2 ⋅ 1 2 + 0 = π 12 ⋅ 12 = π  

Passo 2

Vamos usar a regra de Simpson agora. Como temos o mesmo número de subintervalos,

Temos apenas que moldar a Simpson, Δ x 3 = π 18  

Criando a tabela de pontos,

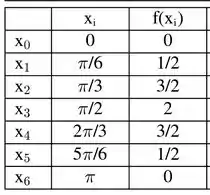
Usando a regra,

T = π 18   ( 0 + 4 ⋅ 1 2 + 2 ⋅ 3 2 + 4 ⋅ 2 + 2 ⋅ 3 2 + 4 ⋅ 1 2 + 0   =   π 18   18 = π  

Resposta

T = π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ - 2 0 ( x 2 - 1 ) d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 1 2 x d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 0 2 sen ⁡ ( x + 1 ) d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 2 4 1 ( s - 1 ) 2 d s com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 0 3 x + 1 d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson