Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.Exercícios de Revisão - Ex. 10
Um circuito em série possui um indutor variável com a indutância definida por:
Encontre a corrente se a resistência é de ohm, a voltagem é e . Esboce o gráfico de .
Passo 1
Então galera, para encontrarmos uma expressão de temos que montar uma equação diferencial antes de tudo, certo? De acordo com as informações dadas pelo enunciado, temos o seguinte:
Separando as variáveis, teremos:
Então agora temos que integrar e resolver!
Passo 2
Integrando, teremos:
O que nos dá como resultado:
Simplificando, teremos:
Para , teremos:
Substituindo na nossa solução:
Passo 3
Agora que encontramos uma solução vamos simplificar para tentar isolar , saca só:
Ufa! Conseguimos isolar como queríamos.
Passo 4
Agora temos que analisar para dois casos: para e para . Para teremos:
Para temos a expressão que encontramos! Sendo assim, nosso resultado será:
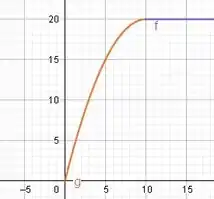
O gráfico disso é:
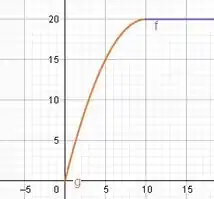
E está aí nossa resposta, galera! 😉
Resposta
