Combine a equação com seu gráfico na figura a seguir e determine as equações para as assíntotas verticais e horizontais.
(a)
(b)
(c)
(d)
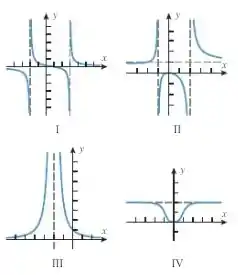
Passo 1
Para cada uma das funções vamos ter que identificar algum ponto chave que nos indique a característica principal da função e, assim, conectar a um dos gráficos.
O mais fácil de se identificar nessas funções são as assíntotas e os zeros das funções. Vamos lá!
Passo 2
(a) )
Onde ocorrem as assíntotas verticais e horizontais?
Para a assíntota vertical, precisamos saber onde a função “explode”, isto é, para qual valor de que a função tende ao infinito. E isso acontece quando temos uma divisão por , geralmente. Pois quando dividimos um número por , essa divisão tende ao infinito, ok?
Para ter uma divisão por :
Fazendo Bháskara:
Dessa forma:
Então, temos assíntotas verticais em e .
Para achar as assíntotas horizontais, devemos saber para qual valor a função tende, quando tende ao infinito. Ou seja, na função:
Quando tem um valor absurdamente grande, a função tende a algum valor específico? Vamos arrumar dessa forma:
Assim, se for gigaaaante, como ele está no denominador de duas frações, essas duas frações vão tender a . Isso porque é como se estivéssemos dividindo por e por , entendeu a ideia? Essas duas divisões seriam praticamente . Dessa forma, com um enorme, temos isso:
Então, é uma assíntota horizontal.
Qual gráfico que bate com essas informações? O único é o II:
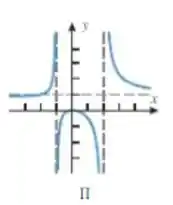
Passo 3
(b)
Mesma coisa: vamos achar as assíntotas.
Para achar a vertical, precisamos que:
Fazendo Bháskara:
Dessa forma:
Então, temos assíntotas verticais em e .
Para achar as assíntotas horizontais, devemos saber para qual valor a função tende, quando tende ao infinito. Ou seja, na função:
Quando tem um valor absurdamente grande, a função tende a algum valor específico? Vamos arrumar dessa forma:
Assim, se for gigaaaante, como ele está no denominador de algumas frações, essas frações vão tender a . Isso porque é como se estivéssemos dividindo por e por , entendeu a ideia? Essas divisões seriam praticamente . Mas, além disso, também temos um sobrando ali no denominador, que vai fazer a função inteira ir para . Dessa forma, com um enorme, temos isso:
Então, é uma assíntota horizontal.
Qual gráfico que bate com essas informações? O único é o I:
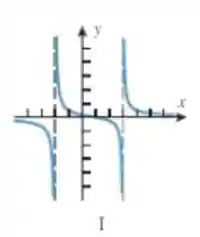
Passo 4
(c)
vamos achar as assíntotas.
Para achar a vertical, precisamos que:
Como não existe número real em que, elevado à quarta potência, resulte num número negativo, não temos assíntotas verticais nessa função.
Para achar as assíntotas horizontais, devemos saber para qual valor a função tende, quando tende ao infinito. Ou seja, na função:
Quando tem um valor absurdamente grande, a função tende a algum valor específico? Vamos arrumar dessa forma:
Assim, se for gigaaaante, como ele está no denominador da fração, essa fração vai tender a . Isso porque é como se estivéssemos dividindo por . Essa divisão seria praticamente . Dessa forma, com um enorme, temos isso:
Então, é uma assíntota horizontal.
Qual gráfico que bate com essas informações? O único é o IV:
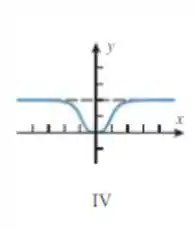
Passo 5
(d)
vamos achar as assíntotas.
Para achar a vertical, precisamos que:
Fazendo Bháskara:
Dessa forma:
Então, temos assíntota vertical em .
Para achar as assíntotas horizontais, devemos saber para qual valor a função tende, quando tende ao infinito. Ou seja, na função:
Quando tem um valor absurdamente grande, a função tende a algum valor específico?
Assim, se for gigaaaante, como ele está no denominador, essa fração vai tender a . Isso porque é como se estivéssemos dividindo por . Essa divisão seria praticamente . Dessa forma, com um enorme, temos isso:
Então, é uma assíntota horizontal.
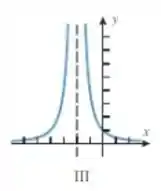
Qual gráfico que bate com essas informações? O único é o III:
Resposta
(a) II
(b) I
(c) IV
(d) III