Encontre uma equação da forma para cada gráfico.

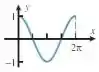
(a) Vamos olhar para o gráfico de novo:

Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:

Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:

Até agora temos:

E o valor de e ? Vamos usar a informação de que a função passa por , substituindo isso em :

E passa pelo ponto :

Substituindo isso na primeira equação:

Sabendo que , temos que:

Sabendo também que (a demonstração se dá fazendo ):

Vamos elevar os dois ao quadrado:

Sabemos que :

E que :

Para isso:

Substituindo em :

Nossa função, então, é:

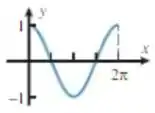
(b) Vamos olhar para o gráfico de novo:

Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:

Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:

Até agora temos:

E o valor de e ? Olha, não conseguimos pegar dois pontos com certeza nesse gráfico... Teríamos apenas e . Só que, fazendo o sistema com esses pontos, encontramos , isso acontece porque , então é como se pegássemos o mesmo ponto duas vezes. Com isso, não conseguimos fazer um sistema para encontrar e .

Mas relaxa, podemos colocar e encontrar uma função que descreva essa curva ainda! Assim, vamos usar esse valor para e o ponto :

Nossa função, então, é:

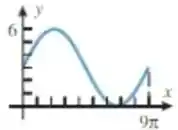
(c) Vamos olhar para o gráfico de novo:

Podemos ver que a função tem seu valor mínimo em e máximo em , logo, sua oscilação é . Com isso, já sabemos sua amplitude:

Além disso, vemos que o tamanho dela é de , logo, esse é o valor do período:

Até agora temos:

E o valor de e ? Vamos usar a informação de que a função passa por , substituindo isso em :

E passa pelo ponto :

Substituindo isso na primeira equação:

Sabendo que , temos que:

Sabendo também que :

Vamos elevar os dois ao quadrado:

Sabemos que :

E que :

Para isso:

Substituindo em :

Já vimos que :

Nossa função, então, é: