Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 54c
Combine as equações polares com os gráficos com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
- ;
- ;
Passo 1
Fala ai, vamos nos divertir resolvendo essa questão? Que tal começarmos analisando a função?
A amplitude da função é igual a 1, temos então uma oscilação então e .
Vamos agora substituir valores em afim de encontrarmos .
Bora lá!
Para
.
Para Para
Para Para
Podemos então com esses pontos entender que os pontos máximos e mínimos podem ser encontrados com os múltiplos de . Vamos começar desenhando o gráfico de .
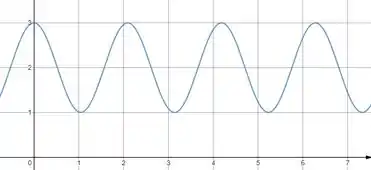
Como podemos ver, não cresce conforme aumenta, o que já nos leva a excluir os dois gráficos espirais. Além disso, não assume valores menores que , o que nos deixa com duas opções: e .
Passo 2
A equação representa uma curva onde o raio varia em função do ângulo , conforme determinado pelo cosseno de . A presença do número dentro do cosseno significa que a curva completa um ciclo completo (ou seja, uma volta completa) a cada radianos de . Isso indica um período de para a curva.
O número de pétalas da curva é determinado pelo coeficiente dentro do cosseno (neste caso, ). A quantidade de pétalas será igual a esse coeficiente, então teremos pétalas para .
O assume valor quando . O ângulo que isso acontece é:
Temos aqui uma situação onde quando . O número dentro do cosseno indica o gráfico onde isso acontece é no gráfico !
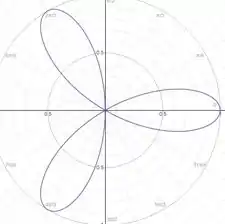
Resposta
O Gráfico correspondente é o .