Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 17
(a) Encontre a excentricidade e a diretriz da cônica
e trace a cônica e sua diretriz.
(b) Se a cônica girar no sentido anti-horário em torno da origem por um ângulo , escreva a equação resultante e trace sua curva.
Passo 1
(a) Bom, galera. Vamos tentar descobrir a excentricidade. Pra isso, a gente tem que comparar a equação do enunciado com uma equação mais geral para cônicas:
Olhando pro denominador, o termo que acompanha é:
Passo 2
Beleza! Pra achar a diretriz, primeiro a gente repara que a equação tem o termo “”, e isso significa que a equação da reta diretriz é da seguinte forma:
Então a gente descobre quem é olhando pro numerador, beleza?
Show! A equação da reta diretriz fica assim:
Bora traçar essa cônica com a diretriz?
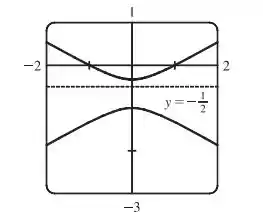
Passo 3
(b) Galera, agora a gente vai ter que rotacionar a cônica de um ângulo e escrevermos uma nova equação pra ela. Mas como a gente faz isso?
Lembre-se do seguinte, se tivermos uma função , e quisermos girar o gráfico dessa função de um ângulo no sentido anti-horário, a nova função vai ser da forma .
Na prática, é só pegar nossa equação original, e tudo que for , a gente substitui por , beleza?
No nosso caso, :
Agora olha a cônica traçada a partir dessa nova equação, veja que ela é uma hipérbole rotacionada, como esperávamos:
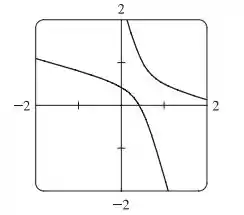
Resposta
(a)
(b)